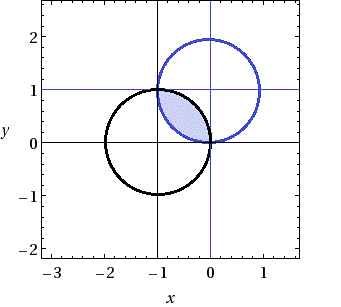
Это определяет собой круг на комплексной плоскости, с центром в точке (0, 1) и радиусом равным 1.

Это определяет открытый круг на комплексной плоскости, с центром в точке (-1, 0) и радиусом равным 1.
На иллюстрации те точки границы множества, которые обозначены черным цветом, не входит в него.