У рівнобедреній трапеції гострий кут дорівнює 30 см .Обчислити площу трапеції , якщо...

Question

Дан 1 ответ

Правильный ответ

Доброго времени суток!

В условии ошибка : "Острый угол равен 30 см". Углы не измеряются в сантиметрах. Скорее всего, Вы имели ввиду 30°.

▔ ▔ ▔

У равнобедренной трапеции острый угол равен 30°. Вычислите площадь этой трапеции, если длины оснований равны 15 см и 23 см.

▔ ▔ ▔

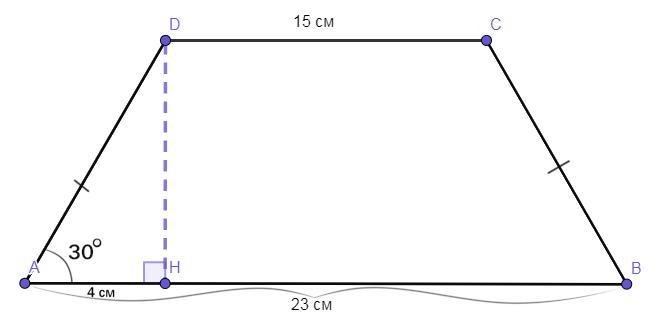
★☆★ Чертёж смотрите во вложении ★☆★

Дано:

Четырёхугольник ABCD — равнобедренная трапеция (AD = CB, CD║AB).

∠DAB = 30°.

CD = 15 см.

АВ = 23 см.

Найти:

S(ABCD) = ?

Решение:

Из вершины ∠ADC на основание АВ опустим высоту DH.

По свойству отрезков, образованных основанием высоты в равнобедренной трапеции, имеем, что —

$AH =\frac{AB-DC}{2}$

Подставим в формулу известные нам значения —

$AH =\frac{23 \ cm-15\ cm }{2}\\\\ AH =\frac{8\ cm }{2}\\\\\boxed {AH =4\ cm}$

Рассмотрим ΔADH — прямоугольный.

$tg(DAH)= \frac{DH}{AH}$

Подставим в формулу известные нам значения —

$tg(30)= \frac{DH}{4\ cm}\\\\\frac{1}{\sqrt{3} } =\frac{DH}{4\ cm}\\\\DH*\sqrt{3} = 4\ cm \\\\ \boxed {DH = \frac{ 4 }{\sqrt{3} } \ cm}$

▸Площадь трапеции равна произведению полусуммы оснований и высоты◂

То есть —

$S(ABCD)=(\frac{CD+AB}{2}) *DH$

Подставим в формулу известные нам значения —

$S(ABCD)=(\frac{15\ cm+23\ cm}{2}) *\frac{4\cm}{\sqrt{3}} \ cm\\\\SABCD)= 19\ cm *\frac{4\cm}{\sqrt{3}} \ cm\\\\ \boxed {S(ABCD)= \frac{76}{\sqrt{3}} \ cm^{2}}$

Ответ:

$\frac{76}{\sqrt{3} } \ cm^{2}$

Lizzie2018_zn (13.1k баллов) 20 Дек, 23