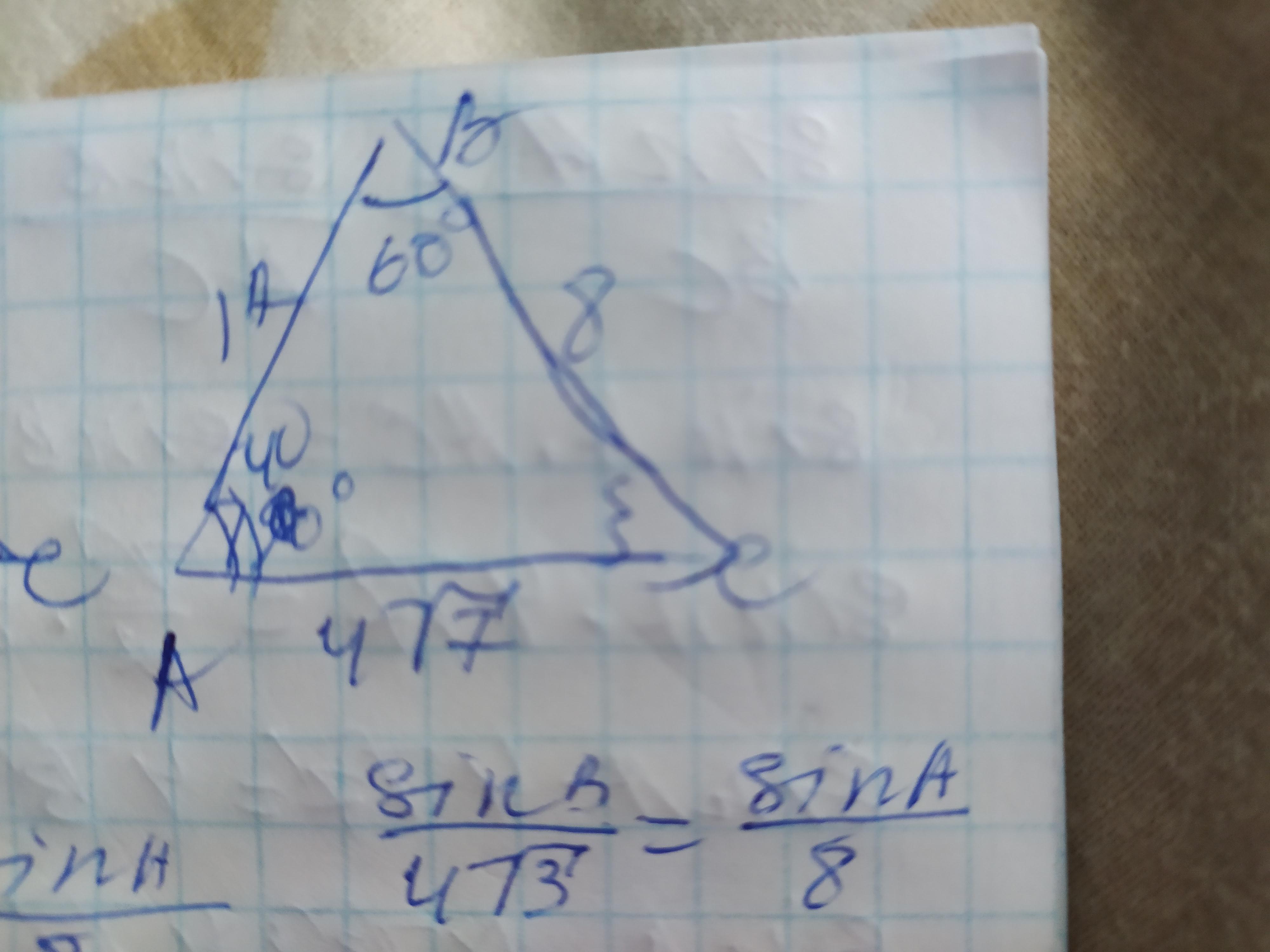Ответ: АС=4√7; угол А=40°; угол С=80°
Объяснение: найдём АС используя теорему косинусов:
АС ²=АВ²+ВС²-2×АВ×ВС×cosB=
=12²+8²-12×8×2×½=144+64-96=112
AC=√112=√16×√7=4√7
По теореме синусов найдём угол А:
sinA/BC=sinB/AC
AC×sinA=BC×sinB
4√7×sinA=8×√3/2
4√7×sinA=4√3
sinA=4√3÷4√7
sinA=√3/√7
Угол А≈40°.
Теперь найдём угол С, зная, что сумма углов треугольника составляет 180°
Угол С=180-60-40=80°