Обчисліть площу фігури, обмеженої лініями y=x²+ 2, y=x+4

Question

Дан 1 ответ

Olga8128_zn · Answer 1 · 2023-12-30T01:13:13+0000

Ответ: $\bold{4,5}$ .

Решение:

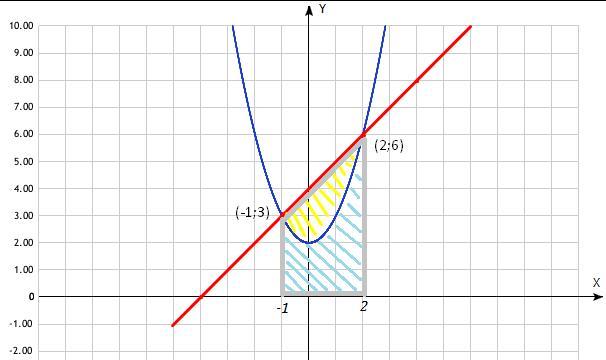
Сначала построим графики обеих функций: параболы $y=x^2+2$ и обычной прямой $y=x+4$ (чертеж смотрите ниже). Точками пересечения будут являться $(-1;3)$ и $(2;6)$ (для того, чтобы их найти, просто решим квадратное уравнение $x^2+2=x-4$ или же $x^2-x-2=0$ теоремой Виета).

Чтобы найти искомую площадь, мы найдем площадь под графиком (выделено светло-голубым и желтым цветом) и площадь обведенной серым трапеции. После из второго вычтем первое и получим то, что нам нужно.

1). Площадь трапеции.

$S_{tr} = 3 \cdot 3 + \dfrac{3 \cdot 3}{2} = 13,5.$

2). Площадь под графиком.

Нам понадобится следующая формула (Ньютона-Лейбница):

$\displaystyle \int\limits^a_b {f(x)} \, dx = F(x) \; |_{a}^{b} = F(b)-F(a).$

Мы будем искать площадь на отрезке $[-1;2]$ :

$\displaystyle \int\limits^2_{-1} {(x^2+2)} \, dx = \bigg (\frac{x^{2+1}}{2+1} + 2 \cdot x \bigg ) dx \;|_{-1}^{\;2} = \bigg (\frac{x^3}{3} + 2x \bigg ) dx \;|_{-1}^{\;2} = \\\\=\bigg (\frac{2^3}{3} + 2 \cdot 2 \bigg ) - \bigg (\frac{(-1)^3}{3} + 2 \cdot (-1) \bigg ) = \frac{8}{3} + 4 + \frac{1}{3} + 2 = 2 + 3 + 4 = 9.$

3). Разность - искомая площадь.

$S = 13,5 - 9 = 4,5.$

Задача решена!

Обчисліть площу фігури, обмеженої лініями y=x²+ 2, y=x+4

Ответ: .

Решение:

Ответ: $\bold{4,5}$ .