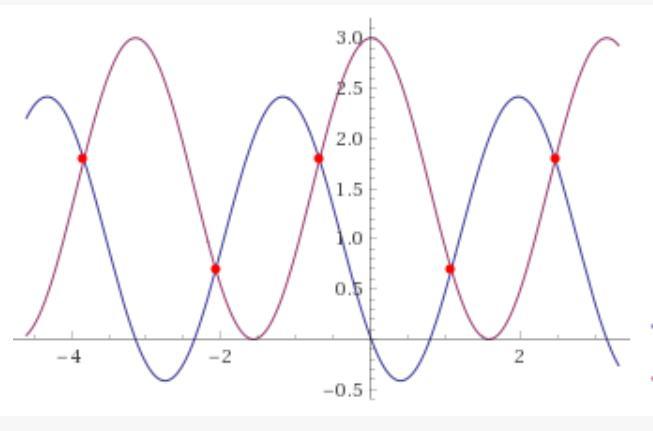
Дано уравнение 2sin²x-2sinxcosx=3cos²x.
Разделим обе части его на cos²x:
2tg² x - 2tg x = 3.
Делаем замену tg x = t.
Получаем квадратное уравнение 2t² - 2t - 3 = 0.
D = 4 + 24 = 28. √D = √28 = 2√7.
t1 = (2 + 2√7)/4 = (1 + √7)/2 ≈ 1,823.
t2 = (2 - 2√7)/4 = (1 - √7)/2 ≈ -0,823.
Обратная замена:
x1 = arc tg(1 + √7)/2 + πk ≈ 1,069 + πk,
x2 = arc tg(1 - √7)/2 + πk ≈ -0,924 + πk.
.