Розв′яжіть нерівність (х^2-5х-14)/(1-x)≥0.

Question

Дано ответов: 2

Wani4kaa_zn · Answer 1 · 2024-01-04T07:31:40+0000

Ответ:

$(-\infty;-2]\cup(1;7]$

Пошаговое объяснение:

Решим неравенство методом интервалов.

$\frac{x^2-5x-14}{1-x}\ge0$

Для начала разложим числитель на множители. Он представлен квадратным уравнением, его можно разложить по следующей формуле:

$ax^2+bx+c=a(x-x_1)(x-x_2)$

Где x₁ и x₂ - решения квадратного уравнения $ax^2+bx+c=0$ .

$x^2-5x-14=0\\D=(-5)^2-4*1*(-14)=25+4*14=25+56=81=9^2\\x_1=\frac{5+\sqrt{9^2}}{2*1}=\frac{5+9}{2}=\frac{14}{2}=7\\x_2=\frac{5-\sqrt{9^2}}{2*1}=\frac{5-9}{2}=\frac{-4}{2}=-2$

$x^2-5x-14=(x-7)(x+2)$

Получаем следующее неравенство:

$\frac{(x-7)(x+2)}{1-x}\ge0$

Введем функцию $f(x)=\frac{(x-7)(x+2)}{1-x}$

Найдем ее область определения:

$D(f): 1-x\ne0\\x\ne1$ (знаменатель дроби не может равняться нулю).

Найдем значения x, при которых функция равна нулю:

$x-7 = 0$ или $x+2=0$

$x=7$ или $x=-2$

Проверяем, подходит ли под область определения (да, подходит).

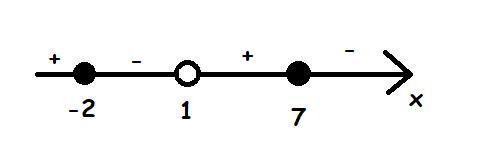
Затем рисуем числовую прямую, обозначаем на ней точки -2 и 7, а также выколотую точку 1.

Эти три точки разделили числовую прямую на 4 интервала, для каждого числа внутри конкретного интервала знак функции будет одинаковым.

Будем брать по одному любому числу для каждого интервала и проверять знак функции.

Возьмем число 8:

0\\8 + 2 > 0\\1 - 8 < 0" alt="8-7 > 0\\8 + 2 > 0\\1 - 8 < 0" align="absmiddle" class="latex-formula">

Количество выражений меньше нуля нечетное, поэтому у функции будет знак меньше нуля.

Возьмем число 3:

$3-70\\1-3$

Количество выражений меньше нуля четное, поэтому у функции будет знак больше нуля.

Возьмем число 0:

0" alt="0-70\\1-0>0" align="absmiddle" class="latex-formula">

Количество выражений меньше нуля нечетное, поэтому у функции будет знак меньше нуля.

Возьмем число -3:

$-3-7$

Количество выражений меньше нуля четное, поэтому у функции будет знак больше нуля.

Итого у нас получилось два интервала, в которых функция принимает значение больше нуля: $(-\infty;-2];(1;7]$