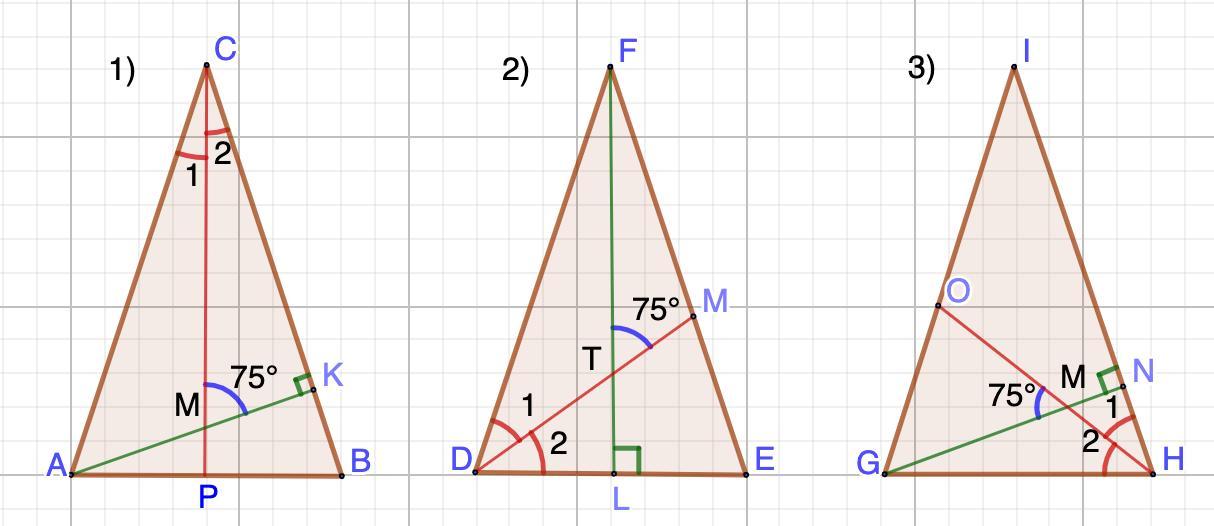
Ответ:
75°;30°;30°.
Объяснение:
1) Проведем биссектрису СР и высоту АК.
ΔМКС - прямоугольный.
∠2=90°-75°=15° (сумма острых углов прямоугольного Δ)
⇒∠С=2·15°=30° (СР - биссектриса)
∠А=∠В (углы при основании р/б Δ)
∠А=∠В=(180°-30°):2=75°
2) FL - высота, DM - биссектриса.
∠FTM=∠DTL=75° (вертикальные)
ΔDTL - прямоугольный
⇒∠2=90°-75°=15° (сумма острых углов прямоугольного Δ)
∠D=∠E=15°·2=30° (DM - биссектриса; углы при основании р/б Δ)
3) НО - биссектриса; GN - высота.
∠OMG=∠NMH=75° (вертикальные)
ΔMNH - прямоугольный
⇒∠1 = 90°-75°=15° (сумма острых углов прямоугольного Δ)
∠G=∠H=15°·2=30° (OH - биссектриса; углы при основании р/б Δ)