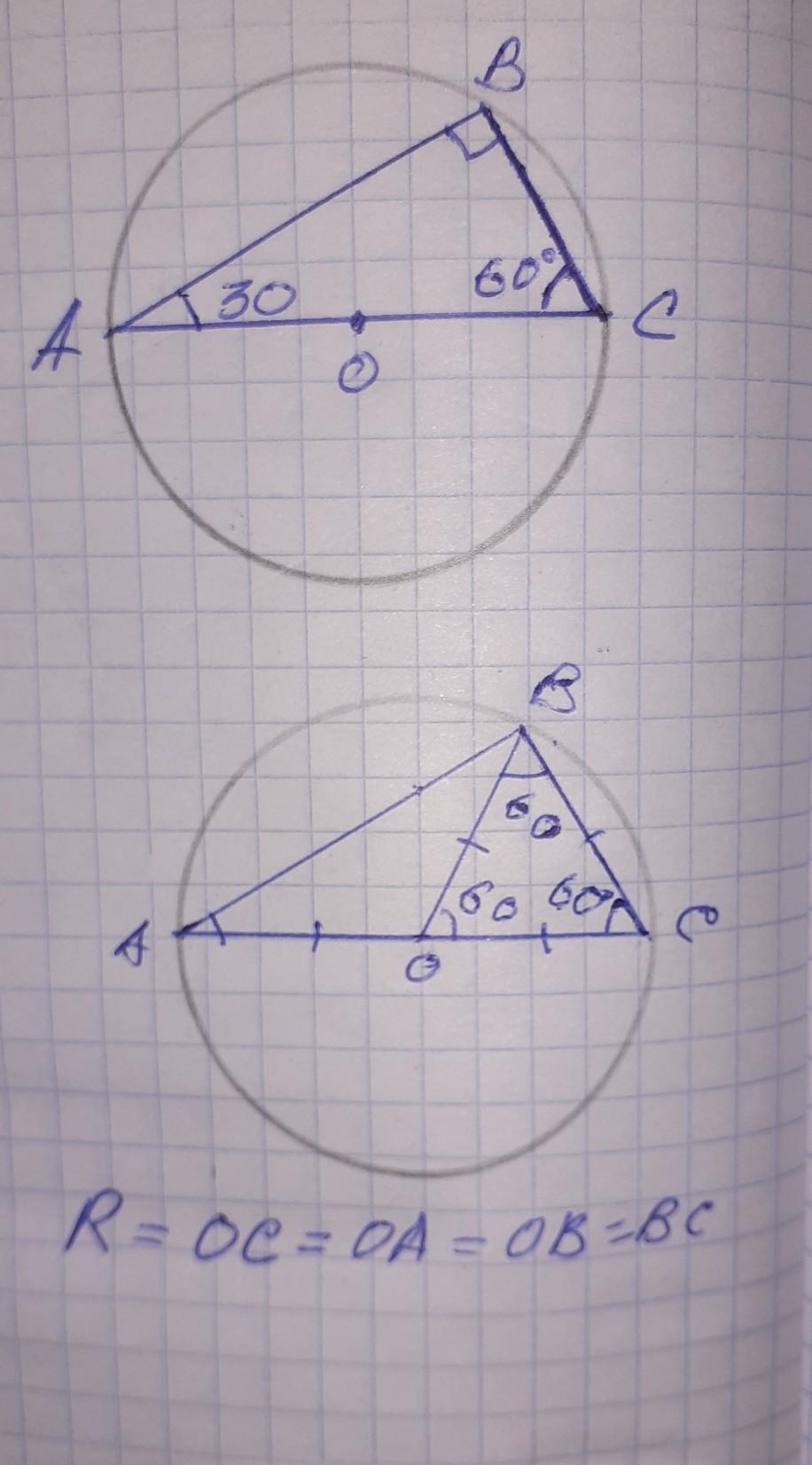
Объяснение:
АС равен диаметру
AC = D=2R =10 см
АВ и ВС хорды
угол между АВ и ВС <ВСО=60° </p>
Диаметр АС , хорды ВС и АВ образуют треугольник Δ ABC .
Радиус ОС =ОА=АС/2=10/2=5 см
расстояние от центра окружности О, до точки хорды В тоже равно радиусу, потому что В лежит в окружности .
<ВСО=60° </p>
Тогда хорда ВС=R=5 см.
Δ ABC прямоугольный, так как у прямоугольного треугольника гипотенуза равна диаметру описанного около него окружности.
Eсли по по-другому сформулировать прямоугольный треугольник - это половина четырёх угольного прямоугольника поделённого на двое диагональю, которое соответственно равно диаметру описанной окружности около четырёх угольного прямоугольника D=d .
<АВС=90° </p>
<ВАО=180°-<ВСО-<АВС=180°-60°-90°=30°</p>
По теореме Пифагора ( катет) хорда АВ=√АС²-ВС²
АВ=√10²-5²=√100-25=√75=√25×3=5√3 см