ПОМОГИТЕ, СРОЧНО! Человек, рост которого составляет 187 см, стоит под фонарём. Его тень...

Ответ:

196,35 cm

Объяснение:

классная задача

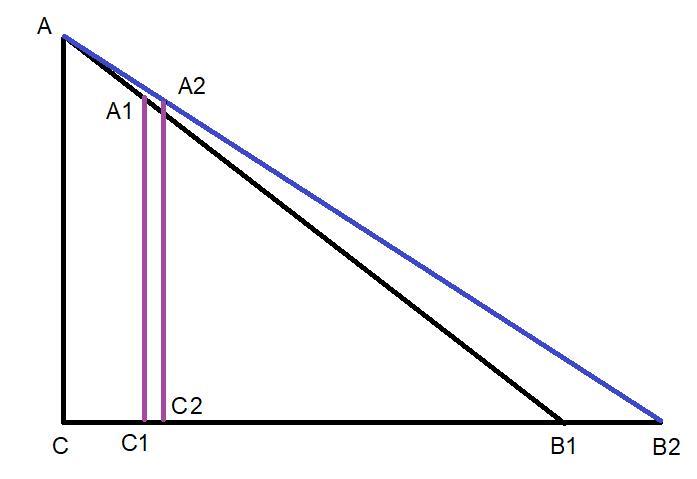
Пусть АС = х

С1С2 = 0,17 м = 1,7 см

А1С1 = А2С2 = 187 см

С1В1 = 168 см

С2В2 = 202 см

Уравнения для решения получаем из равенства тангенсов соответствующих подобных треугольников

1) АС/CB1 = A1C1/C1B1

2) АС/CB2 = A2C2/C2B2

обозначим СС1 = у

Составим систему уравнений, подставив извесные величины

$\left \{ {{\frac{x}{y+168} =\frac{187}{168} } \atop {{{\frac{x}{y+1,7+202} =\frac{187}{202} }} \right.$

из системы находим х, исключая переменную у

$\left \{ {{168x=187(y+168)} \atop {202x=187(y+202+1,7)}} \right.$

$(202-168)x=0 + 187(202+1,7 - 168)$

$34x=187*34+187*1,7$

имеем х=196,35 см

не так уж и высоко был тот фонарь

можно и у посчитать

у = 8,4 см