Ответ:
(см. объяснение)
Пошаговое объяснение:
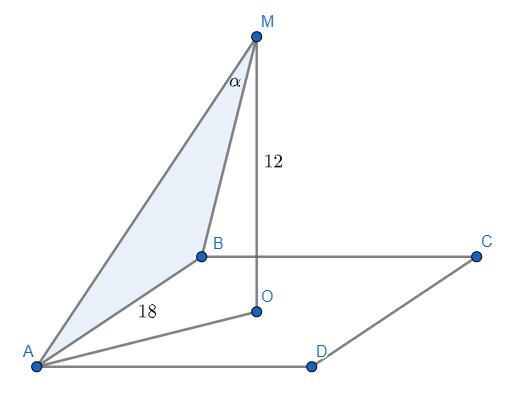
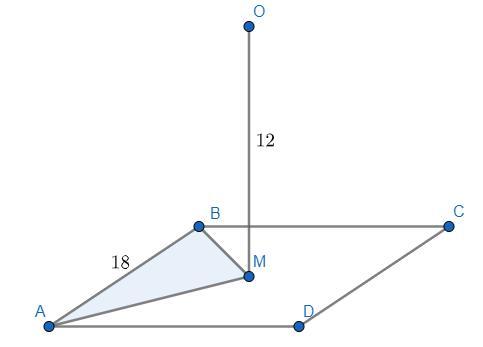
Чертежи приведены ко 2-ому и 3-ему случаям!
Для 1-ого случая можно использовать 1-ый чертеж с введенными в объяснении уточнениями, исключив ненужные построения.
Заметим, что треугольник AOB прямоугольный и равнобедренный. Тогда его высота (назовем ее OH) совпадает с медианой и равна 
. По теореме о трех перпендикулярах MH будет высотой треугольника ABM, а так как OM перпендикулярна плоскости квадрата ABCD, то по теореме Пифагора 
. Откуда 
см².
Приведу другое решение задачи:
Проведем AO. Поскольку OM перпендикулярен плоскости, то ΔAOM прямоугольный. Заметим, что AO - половина диагонали квадрата, так как точка O - центр квадрата.
Найдем AO:
AO=9\sqrt{2}" alt="x^2=18^2+18^2\\x^2=648\\x=18\sqrt{2}\\=>AO=9\sqrt{2}" align="absmiddle" class="latex-formula">
По теореме Пифагора для ΔAOM:
Аналогично 
, так как диагонали квадрата равны.
Искать площадь по формуле Герона не удобно, так как получили значения с корнями.
Поэтому воспользуемся теоремой косинусов:
\sin\alpha = \dfrac{15}{17}" alt="18^2=(3\sqrt{34})^2+(3\sqrt{34})^2-2\times(3\sqrt{34})^2\times\cos\alpha\\\cos\alpha=\dfrac{8}{17}\\=>\sin\alpha = \dfrac{15}{17}" align="absmiddle" class="latex-formula">
Тогда площадь треугольника ABM равна:
Получили, что площадь треугольника ABM равна 135см².
Замечу, что в задаче не указано, что центр квадрата - это точка O. Так принято. Однако возможен другой случай, где эти точки поменяны местами. Тогда 
. Единицы измерения см².
