Ответ:
4 см.
Объяснение:
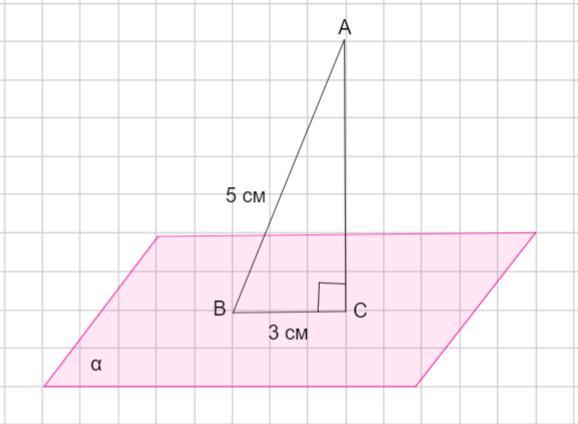
К плоскости α проведена наклонная, длина которой равна 5 см, проекция наклонной равна 3 см . На каком расстоянии от плоскости находится точка, из которой проведена наклонная?
Пусть дана плоскость α. Из точки А проведена наклонная АВ . Тогда если АС ⊥α, то АС - перпендикуляр к плоскости, проведенный из точки А. Тогда ВС - проекция наклонной АВ на плоскость α.
ΔАСВ - прямоугольный, гипотенуза АВ = 5 см, катет ВС = 3 см.
Найдем катет АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АВ²= ВС ² +АС ²;
АС²=АВ²- ВС ²;
АС² = 5² - 3² = 25 - 9 = 16;
АС =√16 = 4 см.
Расстоянием от точки до плоскости - это длина перпендикуляра, опущенного из этой точки на плоскость, то есть это длина катета АС. Значит, расстояние от точки до плоскости равно 4 см.
#SPJ1