Ответ:
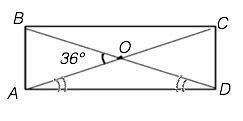
1) ∆ АОD - равнобедренный, углы при его основании равны
Для ∆ АОD угол АОВ по свойству внешнего угла треугольника равен сумме не смежных с ним углов: ∠ОАD +∠ODA=36°
∠САD=∠ODA=36°:2=18°
Угол АDC=90°, ⇒ ∠BDC=∠ADC-∠ODA=90°-18°=72°
2) Так как угол АDC - прямой то угол ADC=40°, а угол CDB=50°.
Так как диагонали прямоуголник равны и точкой пересечения делятся пополам, то треугольник АОВ равнобедренный, следовательно угол АВD=50° и угол ВАО=50°, тогда угол ВОА=180°-100°=80°
Пошаговое объяснение: