Ответ: Р=34см
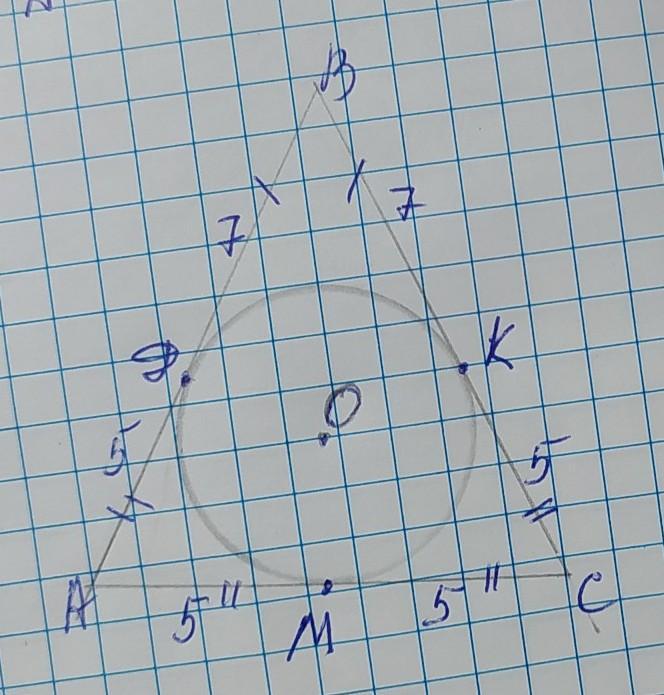
Объяснение: обозначим центр окружности т.О, вершины треугольника А В С, а точки касания Д К М. Причём Д ∈ АВ; К ∈ ВС; М ∈ АС. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных, соединяясь в одной вершине равны, от точки касания до вершины треугольника. Поэтому ВД=ВК=7см; АД=АМ=5см; СК=СМ=5см → АД=АМ=СК=СМ=5см. Теперь сложим эти отрезки сторон:
АВ=ВС=5+7=12см; АС=АМ+СМ=5+5=10см.
Зная все стороны треугольника найдём его периметр: Р=АВ+ВС+АС=12+12+10=24+10=
=34см