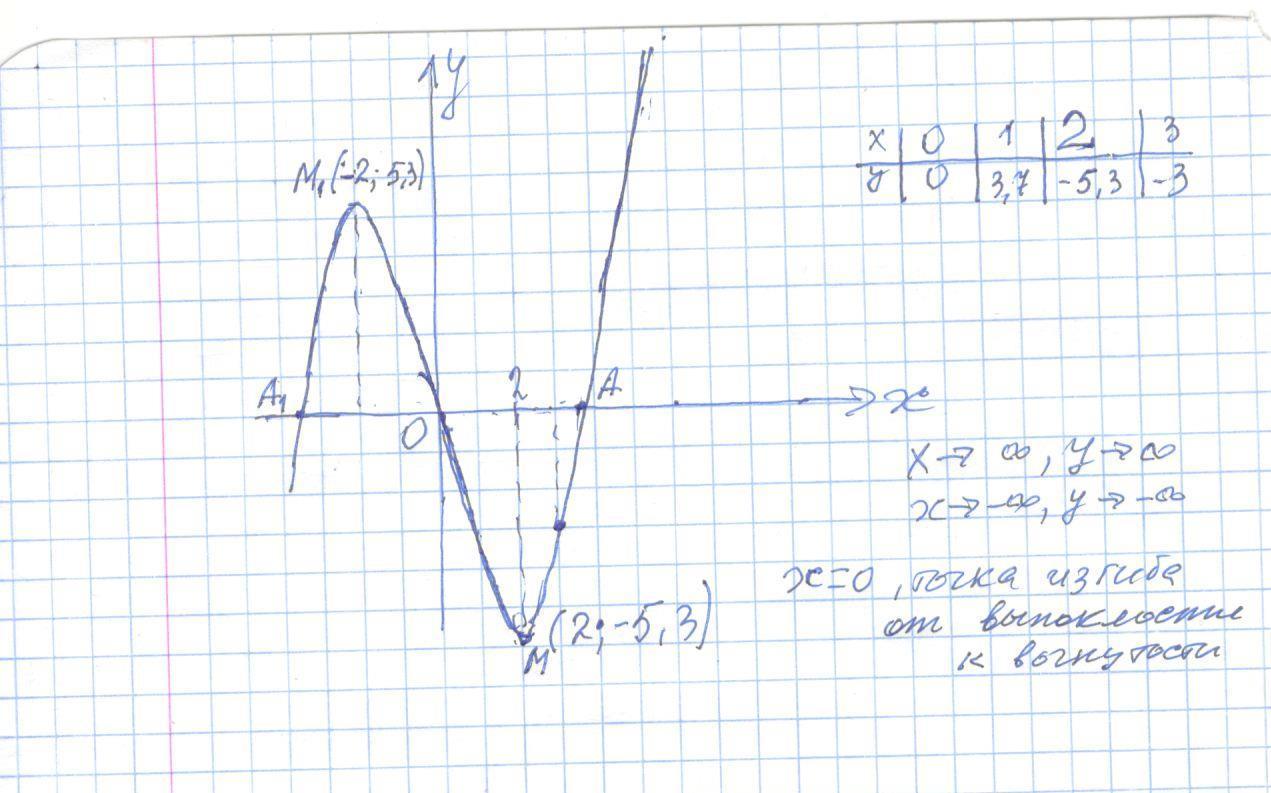
Найти интервалы возрастания, убывания функции , точки экстремума и схематично построить ее график :
y = x³/3 - 4x
Ответ:
Объяснение:
1. ООФ : x ∈ R ;
2. Функция нечетная.
Действительно : y(-x) =(-x)³/3 - 4*(-x) =-x³/3 + 4x = - (x³/3 - 4x) = - y(x)
График нечетной функции симметричен относительно начала координат. Заметим, что график нечетной функции достаточно исследовать только при x ≥ 0, а при x<0 достроить по симметрии, т.е. симметрично относительно начала координат.</p>
Функция непериодическая.
3. Определим точки пересечения графика функции с осями координат
Точки пересечение графика функции с осью ординат( x=0) :
y =0 ; [ y =0³/3 -4*0 = 0 ] O(0;0)
Точки пересечение графика функции с осью абсцисс ( y=0) :
x³/3 - 4x = 0 ⇔(1/3)*(x² - 12) = (1/3)*x (x +2√3)(x -2√3) =0
x₁ =2√3 ; x₂ = - 2√3 ; x₃=0. [ A(2√3 ; 0) , A₁( -2√3 ; 0) ; O(0;0) ]
2√3 ≈ 3, 46
4. Найти интервалы возрастания, убывания функции, точки экстремума:
y ' =(x³/3 - 4x) = x² -4 = (x+2)(x-2)
Функция убывающая(↓) ,если y ' ≤ 0 , возрастающая(↑) ,если y ' ≥ 0
y ' + + + + + + + + + + [ -2 ] - - - - - - - - - - - - [2] + + + + + + + + + +
y ↑ (возрастает) max ↓ (убивает) min ↑
y(-2)= (-2)³/3 -4*(-2) = 16/3 ≈ 5 ,3 → точка максимума M₁( -2 ; 5,3)
y(2)= 2³/3 - 4*2 = - 16/3 ≈ - 5 ,3 → точка минимума M( 2 ; -5,3)
[ y( -x) = -y(x) ]
5. Найти точки перегиба ( y '' =0 ) :
y '' =(y ') ' =(x² - 4) ' =2x ; y '' =0 ⇒ x=0
график функции выпуклая , если y ' ' <0 x ∈( - ∞ ; 0)</p>
график функции вогнутая , если y ' ' > 0 x ∈( 0 ; ∞ )
Схематический график функции см приложение