Дам 60 баллов!!! Точки A и B делят окружность с центром O ** дуги AMB и ACB так, что дуга...

Question

Дам 60 баллов!!! Точки A и B делят окружность с центром O на дуги AMB и ACB так, что дуга ACB в 2 раза меньше дуги AMB. AM – диаметр окружности. Найдите углы AMB, ABM, ACB. С чертежом и решением

Answer 1

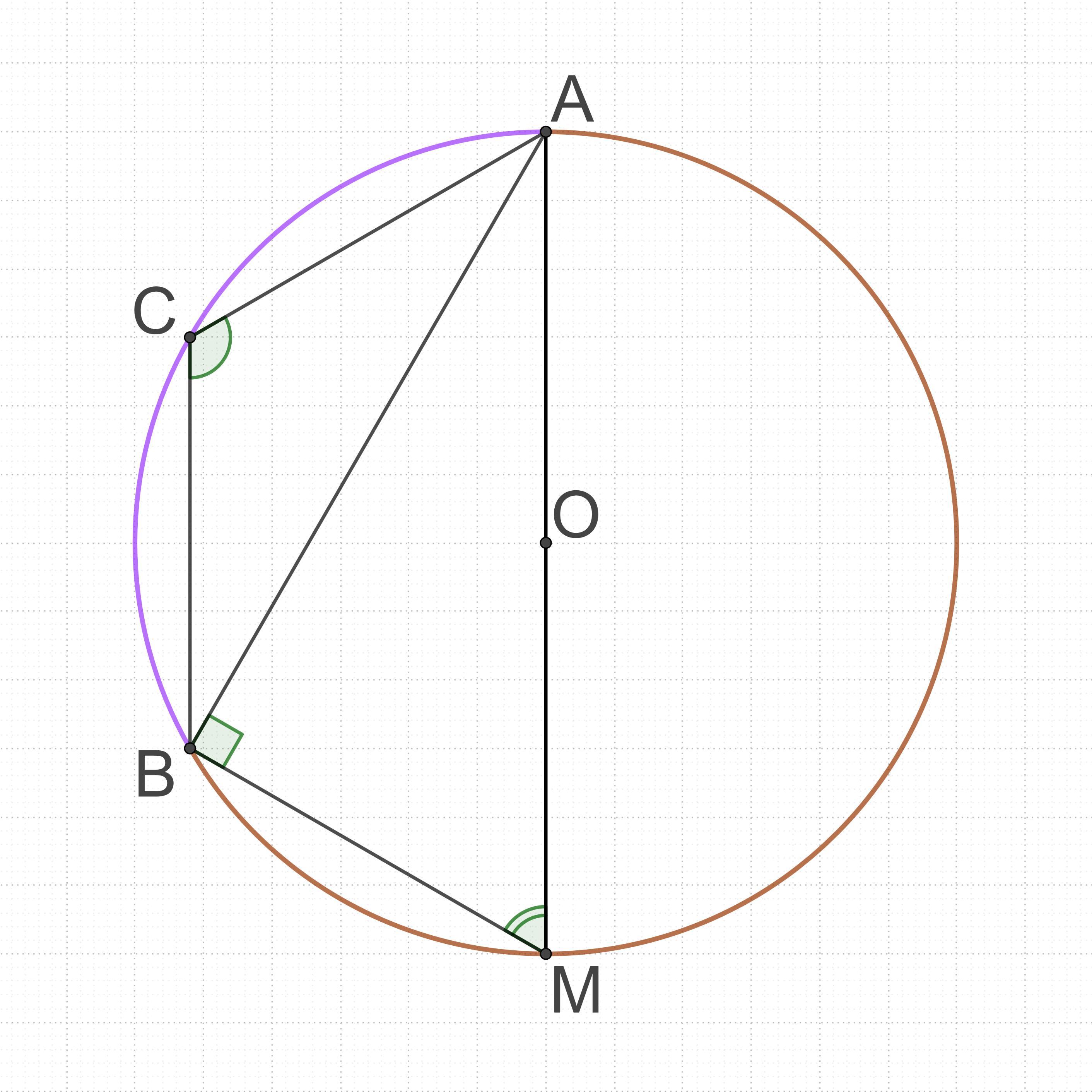
Решение:

1) Найдем градусные меры данных дуг:

∪AM = 360/2 = 180°

• ∪ACB — x°
• ∪AMB — 2x°

    ∪ACB + ∪AMB = 360°

    x+2x = 360

    3x = 120

∪ACB — x = 120°

∪AMB — 2x = 2·120 = 240°

2) Найдем градусные меры углов, исходя из свойства вписанного угла (вписанный угол равен половине дуги, на которую опирается).

∠ABM = 1/2·∪AM = 180/2 = 90°

∠ACB = 1/2·∪AMB = 240/2 = 120°

∠AMB = 1/2·∪ACB = 120/2 = 60°

Ответ:

• ∠AMB = 60°;
• ∠ABM = 90°;
• ∠ACB = 120°.

---

Comments

Спасибо