Ответ: 5
Объяснение:
Классная задачка! Требует минимум знаний геометрии.
Попробую рассказать что я делал. Тут везде середины отрезков и ничего конкретного более не сказать. Медиана делит треугольник на равные по площади треугольники. Значит надо это использовать.
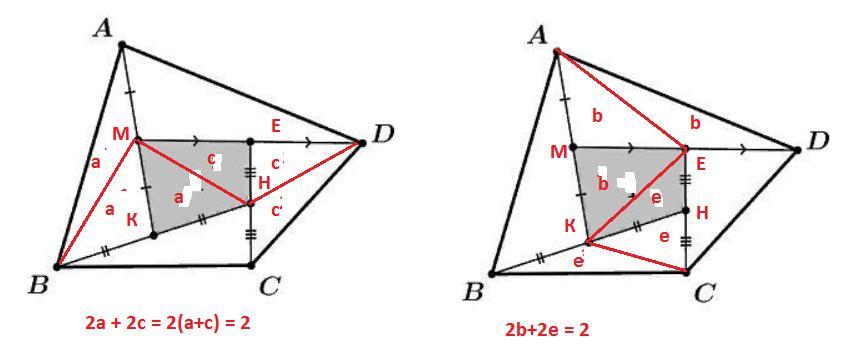
Я разделил диагональю МН закрашенное на две части. Значит и площадь разделена на две части. Единственное, что мы знаем об этих площадях - их сумма равна 1. Мне лень обозначать площади S₁ и S₂, поэтому площадь первой части я обозначил а, а второй с. Если сложить а+с = 1. Я построил треугольник ВМН. Медиана МК делит его на два равновеликих треугольника с равной площадью. Если площадь одного а, то и другого а. Из треугольника АВК видно, что и АМВ имеет площадь а.Значит треугольники АВК и СЕД в сумме имеют площадь 2
Потом построил треугольник МСВ и аналогичными суждениями получил, что площадь АМД+площадь СЕД = 2
Тогда площадь всего четырехугольника = 5