Знайдіть площу трикутника ABC, якщо AC = √5 см, ВС = √10 AB=√13.

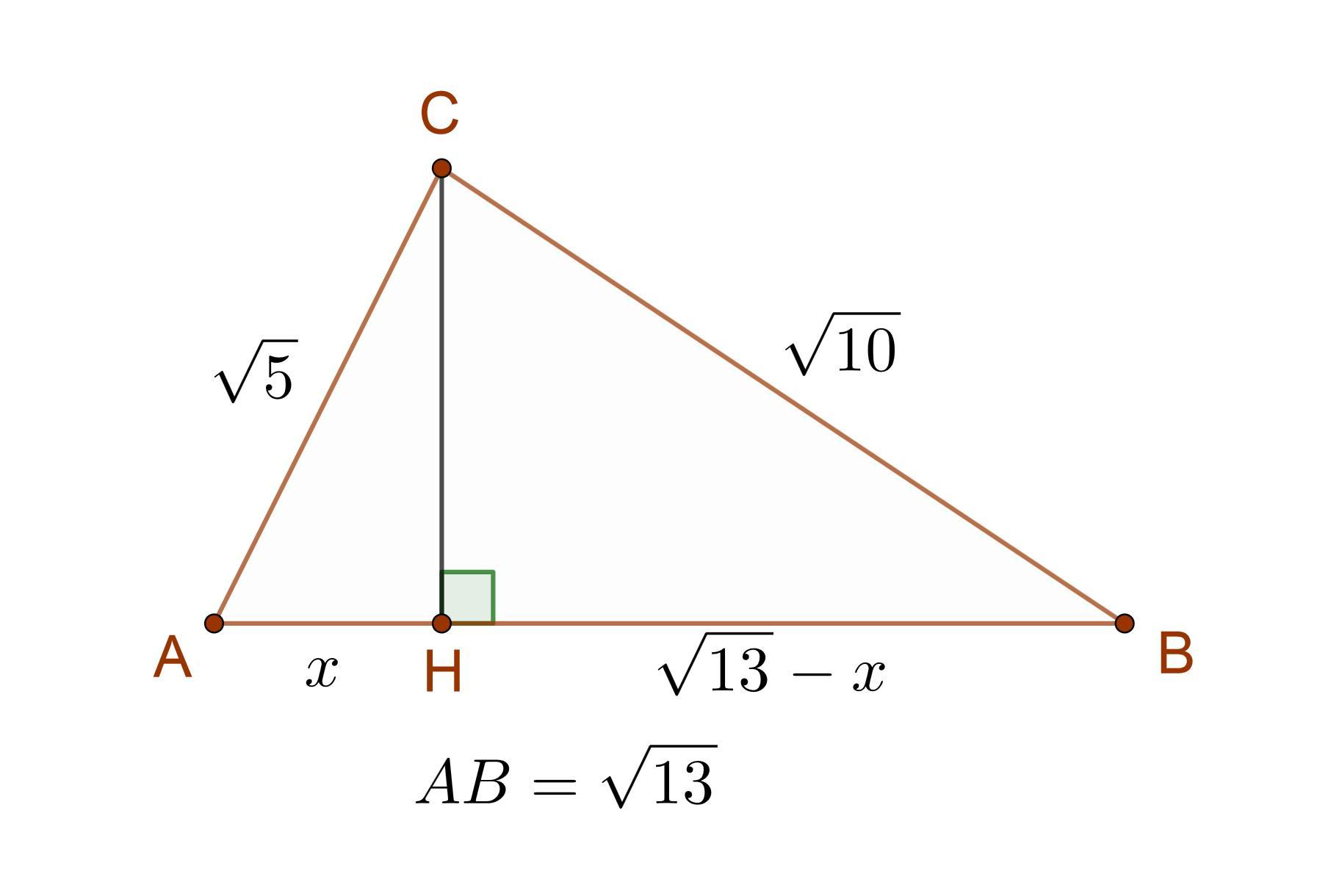
Розв'язок:

Опустимо висоту CH з вершини C на сторону AB.

Тоді відрізок AH = x cm, а відрізок BH = √13−x cm.

Виразимо висоту CH з прямокутних трикутників ACH та BCH за т. Піфагора:

$CH^2 = AC^2-AH^2\\CH^2 = BC^2-\left(\sqrt{13}-AH\right)^2\\$

Зрівняємо праві частини рівнянь:

$AC^2-AH^2 = BC^2-\left(\sqrt{13}-AH\right)^2$

Підставимо значення та знайдемо невідому змінну:

$\left(\sqrt{5}\right)^2-x^2 = \left(\sqrt{10}\right)^2-\left(\sqrt{13}-x\right)^2\\5-x^2 = 10-\left(13-2\sqrt{13}x+x^2\right)\\5-x^2 = 10-13+2\sqrt{13}x-x^2\\2\sqrt{13}x=8\\x=\frac{8}{2\sqrt{13}} = \frac{4}{\sqrt{13}}$

Тобто, AH = x = 4/√13 cm.

Знайдемо довжину висоти CH за т. Піфагора з ΔACH:

$CH=\sqrt{AC^2-AH^2} \\CH=\sqrt{\left(\sqrt{5} \right)^2-\left(\frac{4}{\sqrt{13} }\right)^2} = \sqrt{5-\frac{16}{13} } =\sqrt{3\frac{10}{13} } =\sqrt{\frac{49}{13} } = \frac{7}{\sqrt{13} } \:\: (cm)$

Підставимо значення у формулу площі трикутника:

$S_{\triangle ABC} = \frac{AB\cdot CH}{2} \\S_{\triangle ABC} = \frac{1}{2}\sqrt{13} \cdot \frac{7}{\sqrt{13}} = \frac{7}{2} = 3.5 \:\: \left(cm^2\right)$

Відповідь: Площа трикутника ABC рівна 3.5 cm².