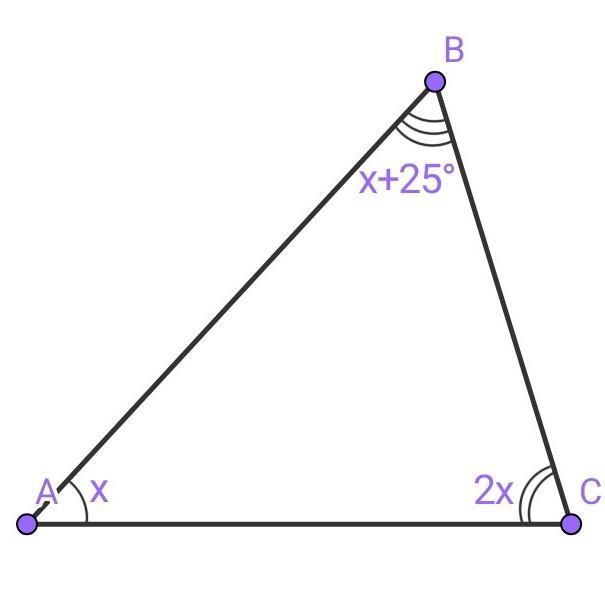
Найдите углы треугольника, если один из них вдвое больше другого и на 25° меньше третьего.
— — —
Дано :
∆АВС.
∠А <</em> ∠С в 2 раза.
∠А <</em> ∠В на 25°.
Найти :
∠А = ?
∠В = ?
∠С = ?
Решение :
Пусть ∠А = х, тогда, по условию задачи, ∠В = х + 25°, а ∠С = 2х.
- Сумма углов треугольника равна 180°.
Составим уравнение —
∠А + ∠В + ∠С = 180°
х + (х + 25°) + 2х = 180°
х + х + 25° + 2х = 180°
4х + 25° = 180°
4х = 155°
х = 38,75°.
∠А = х = 38,75°
∠В = х + 25° = 38,75° + 25° = 63,75°
∠С = 2х = 2*38,75° = 77,5°.
Ответ :
38,75°, 63,75°, 77,5°.