Ответ:
Примерно так:
Объяснение:
1. Что такое ломаная? Что такое звенья, вершины и длина ломаной?
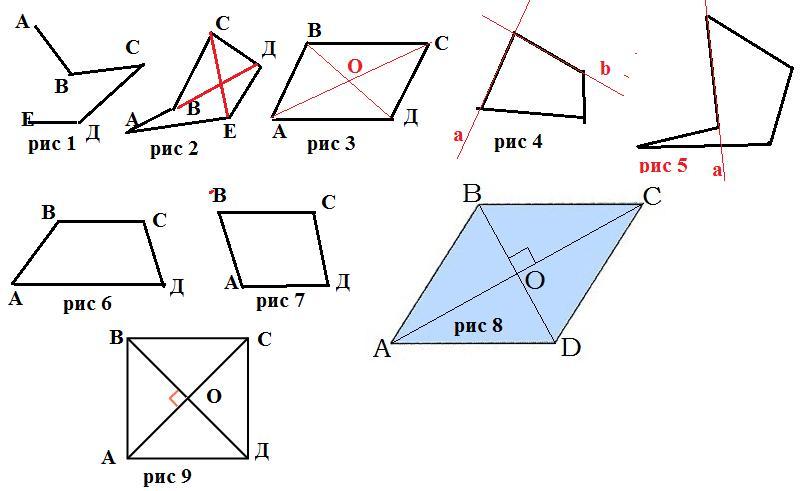
Возьмем несколько отрезков и последовательно соединим концы этих отрезков и получим ломаную (рис 1). Можем дать такое определение:
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом другого.
Каждый отрезок, из которых состоит ломаная, называется звеном, например АВ, ВС и тд
2. Что такое многоугольник? Что такое вершины, стороны, периметр и диагонали многоугольника?
Если два свободных конца ломаной замкнуть, то получится многоугольник (рис 2). Можно дать такое определение:
Многоугольник - это часть плоскости ограниченная замкнутой ломаной.
Точки, в которых соединяются звенья ломаной называются вершинами (А,В,С и тд).
Каждый отрезок замкнутой ломаной называется стороной многоугольника.
Сумма длин всех сторон называется периметром.
Отрезки, соединяющие две не соседние вершины называются диагоналями (например на рис 2 СЕ и ВД)
4. Чему равна сумма углов выпуклого четырёхугольника?
Сумма внутренних углов выпуклого четырехугольника равна 360 градусам.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины (рис 4). Не выпуклый многоугольник
на рис 5
5.Дайте определение параллелограмма, перечислите его свойства и признаки.
Параллелограмм (рис 3) - это четырехугольник, у которого противолежащие (противоположные) стороны попарно параллельны.
Свойства:
1. Противоположные стороны и противоположные углы параллелограмма равны.
2. Диагонали (рис 3 АС и ВД) параллелограмма в точке пересечения (точка О) делятся пополам.
Кроме этих есть не канонизированные Атанасяном но весьма полезные свойства:
3. Любая диагональ параллелограмма делит его на два равных треугольника.
4. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
5. Сумма углов, прилегающих к любой стороне равна 180 градусам.
Признаки - это те особенности, по которым мы опознаем параллелограмм:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то этот четырехугольник параллелограмм.
6. Какой четырёхугольник называется трапецией, как называются её стороны?
Четырехугольник, у которого две стороны параллельны, а две другие нет, то этот четырехугольник - трапеция (рис 6 и рис 7 ВС и АД основания, АВ и СД - боковые стороны).
Параллельные стороны называются основаниями, а не параллельные боковыми сторонами.
7. Какая трапеция называется равнобедренной, прямоугольной? Какими свойствами обладает равнобедренная трапеция?
Равнобедренной называется трапеция, у которой боковые стороны равны между собой.
Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна обоим основаниям.
Свойств много, напишу чаще применяемые:
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
3. Вокруг равнобедренной трапеции можно описать окружность
4. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
5. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
6. Сумма углов прилегающих к боковым сторонам равна 180 градусам.
8. Какой четырёхугольник называется прямоугольником? Перечислите его свойства.
Четырехугольник, у которого все углы прямые (равны 90 градусам) называется прямоугольником.
Прямоугольник обладает всеми свойствами параллелограмма (смотрите выше) и кроме того:
1. Диагонали прямоугольника равны.
2. Диагонали в точке пересечения делятся на равные отрезки.
3. Вокруг любого прямоугольника можно описать окружность, и при этом его диагонали являются диаметрами этой окружности.
9. Какой четырёхугольник называется ромбом? Перечислите его свойства
Ромбом (рис 8) называется параллелограмм у которого все стороны равны.
Ромб обладает всеми свойствами параллелограмма, и сверх этого:
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба являются биссектрисами его углов.
3. Диагонали делят ромб на 4 равных прямоугольных треугольника.
10. Какой четырёхугольник называется квадратом? Перечислите его свойства
Прямоугольник, у которого все стороны равны называется квадратом.
Квадрат обладает всеми свойствами прямоугольника и сверх этого:
1. Диагонали квадрата перпендикулярны.
2. Диагонали квадрата являются биссектрисами его углов.
3. Диагонали делят квадрат на 4 равных прямоугольных треугольника.