В равнобедренном треугольнике ABC угол ABC равен 120° . Высота BK , проведённая к...

$60$ ед.

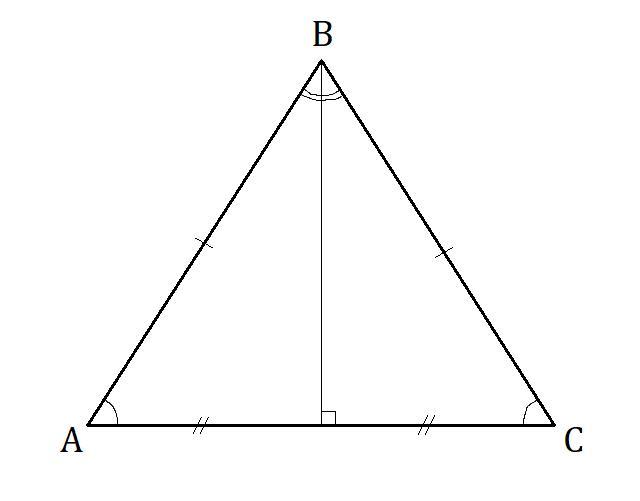
Высота , проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является биссектрисой и медианой.

⇒ $BK$ - высота, медиана, биссектриса.

$\angle ABK = \angle CBK = \dfrac{\angle ABC}{2} = \dfrac{120^{\circ}}{2} = 60^{\circ}$ , так как $BK$ - биссектриса.

$\triangle ABK$ - прямоугольный, так как $BK$ - высота.

Сумма острых углов прямоугольного треугольника равна $180^{\circ}$ .

⇒ $\angle BAK = 90^{\circ} - \angle ABK = 90^{\circ} - 60^{\circ} = 30^{\circ}$ .

Если угол прямоугольного треугольника равен $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

⇒ $AB = 2 \cdot BK = 2 \cdot 30 = 60$ ед.

А так как $\triangle ABC$ - равнобедренный ⇒ $AB = BC = 60$ ед.