Прямокутний трикутник із катетами 9 см і 12 см обертається навколо більшого катета....

Question

Дан 1 ответ

Правильный ответ

Ответ:

Площадь полной поверхности тела вращения 216πсм².

Объяснение:

Прямоугольный треугольник с катетами 9 см и 12 см вращается вокруг большего катета. Найти площадь полной поверхности поученного тела вращения.

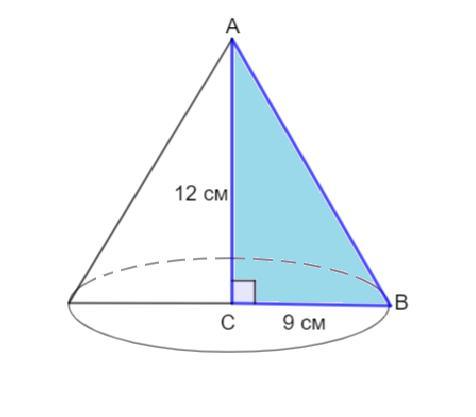
Пусть дан Δ АВС -прямоугольный.

Катеты АС =12 см, ВС =9см.

Если прямоугольный треугольник вращается около катета, то телом вращения будет конус.

Если треугольник вращается вокруг наибольшего катета, то этот катет - высота конуса, а меньший катет радиус основания конуса.

Применим к ΔАВС теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Найдем гипотенузу АВ, которая является образующей конуса.

$AB^{2} =AC^{2} +BC ^{2} ;\\AB =\sqrt{AC^{2} +BC ^{2}} ;\\AB =\sqrt{12^{2}+9^{2} } =\sqrt{144+81} =\sqrt{225} =15$ см.

Площадь полной поверхности конуса равна сумме площади боковой поверхности и площади основания.

S полн.=S бок.+Sосн.

Боковая поверхность конуса определяется по формуле

S бок.= πRl, где R -радиус основания конуса, l- образующая.

$S =\pi \cdot 9\cdot 15 =135\pi$ см².

В основании конуса круг радиуса 9 см. Найдем площадь круга по формуле:

$S =\pi R^{2} ,$ где R -радиус

$S=\pi \cdot 9^{2} =81\pi$ см².

Тогда площадь полной поверхности конуса

Sполн. =135π +81π= 216πсм².

#SPJ5

lilyatomach_zn (5.5k баллов) 06 Апр