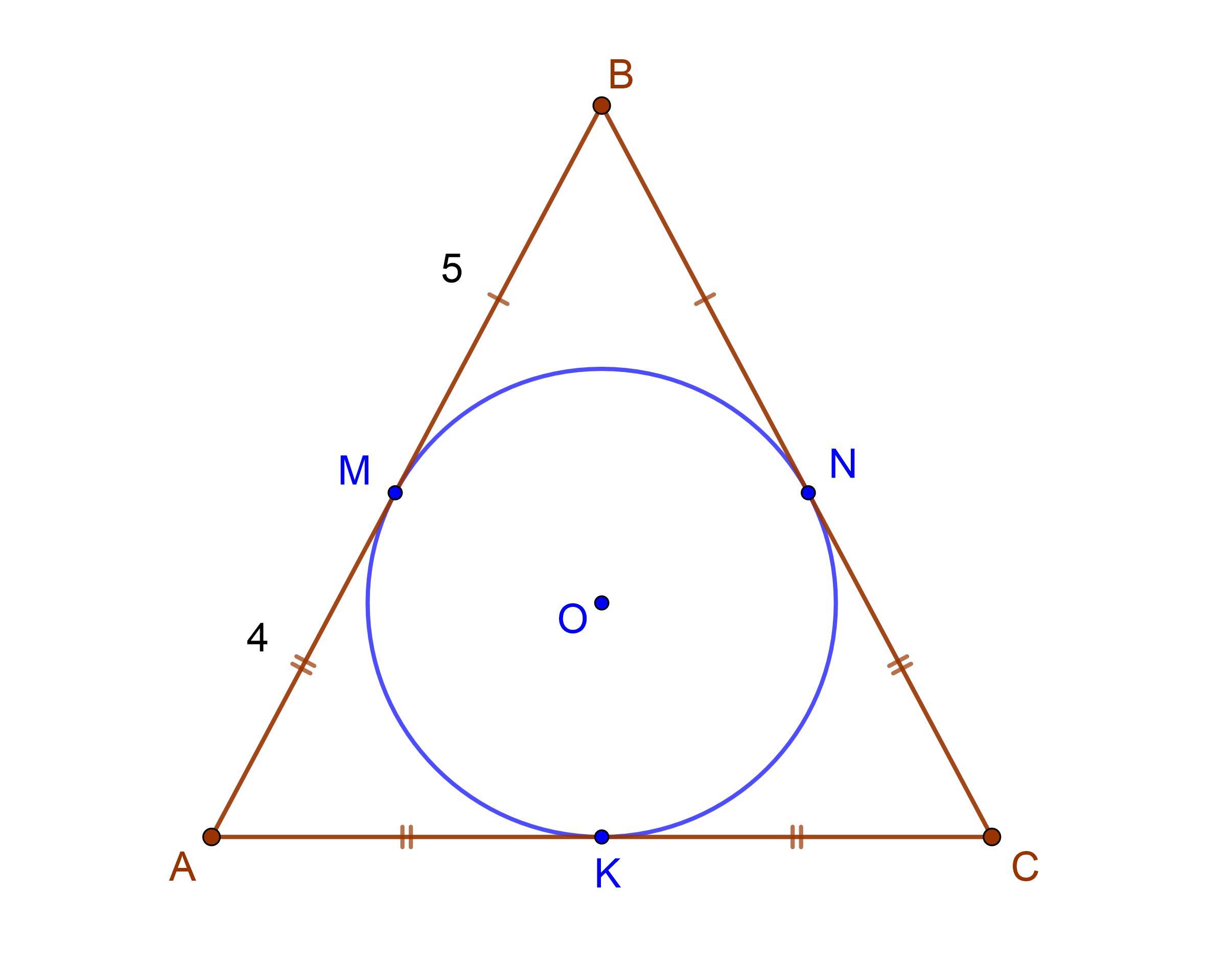
Задача: В равнобедренном треугольнике АВС с основанием АС вписана окружность, причем М — точка касания, которая делит боковую сторону на отрезки длиной 4 см и 5 см. Найти периметр треугольника.
Решение:
Точки M, N и K — точки касания вписанной окружности.
Длины касательных к окружности, проведенных с общей точки, равны. Так как ΔABC равнобедренный с основанием AC, тогда:
BM = BN = 5 (см)
AM = AK = CK = CN = 4 (см)
AC = AK+CK = 4+4 = 8 (см)
AB = CB = AM+BM (CN+BN) = 4+5 = 9 (см)
P = AC+2·AB = 8+9·2 = 8+18 = 26 (см)
Ответ: Периметр треугольника равен 26 см.