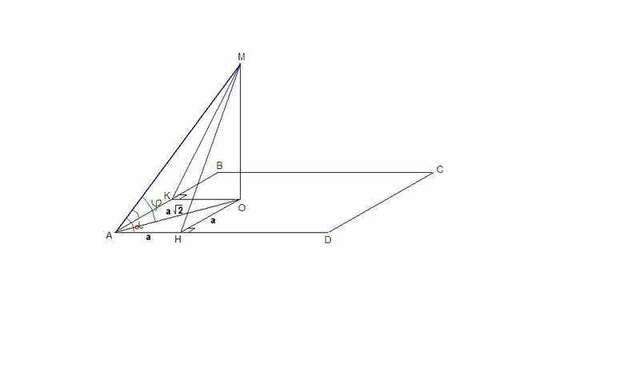
Пусть МО⊥(АВС).
Проведем ОН⊥AD и ОК⊥АВ.
ОН и ОК- проекции наклонных МН и МК на плоскость прямоугольника, тогда и МН⊥AD, МК⊥АВ по теореме о трех перпендикулярах.
∠МАО = φ - угол между наклонной АМ и плоскостью прямоугольника,
∠МАН = ∠МАК = α = 50° - угол между наклонной АМ и сторонами AD и АВ прямоугольника.
ΔМАН
= ΔМАК по гипотенузе и острому углу (АМ общая, ∠МАН = ∠МАК = α), значит
АК = АН, и значит АКОН - квадрат и АО - его диагональ, а следовательно и
биссектриса угла BAD.
Стоит запомнить, что наклонная,
проведенная через вершину угла, лежащего в плоскости, и образующая
равные углы с его сторонами, проецируется на биссектрису этого угла.
Пусть а - сторона квадрата АКОН.
Тогда АО = а√2, как диагональ квадрата.
ΔАМН: АМ = AН / cosα = a / cos α
ΔAMO: cos φ = АO / AM = a√2 / (a / cos α) = √2cos α
cosφ = √2cos50°
φ = arccos(√2cos50°)