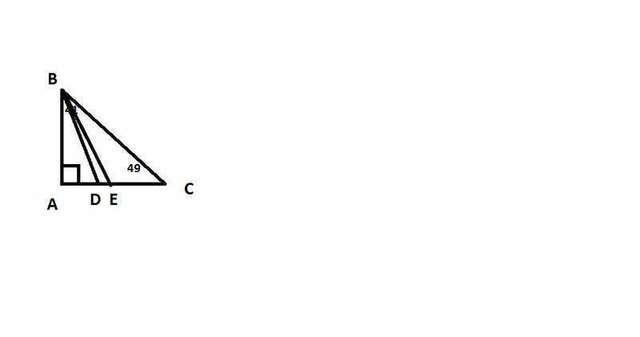Сумма уголов=180
углы= 90, 49 , 41 градусов
см. рисунок
BD- биссектрисса
углы ABD=DBC=41/2=20.5 градусов
BE- медиана
Строим треугольник, пусть АВ=1
АС=АВ/тангенс 41=1/0,8692=1,15
Смотрим треугольник АВЕ
АВ=1
АЕ=АС/2=0,575
узнаем тангенс угла BEA =AE/AB=0.575/1=0.575
угoл BEA=29.9 градусов
29,9-20,5=9,4 градуса
---------------------------------------------------------------------------------------------------------------------
Если бисс. и медиану ведем из прямого угла, то
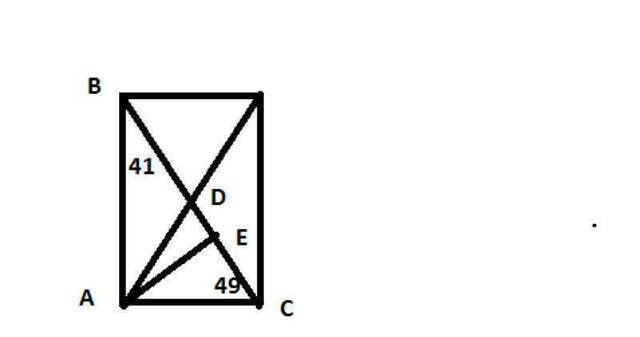
СМ. Рисунок
АЕ- биссектриса
угол САЕ=90/2=45
АD- медиана
Достроим до прямоугольного четырехугольника
треугольник АВD- равностронний, значит
уголы ABC=DAB=41
45-41=4 градуса