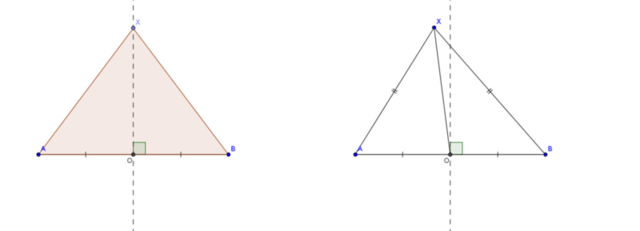
Можно доказать, что гмт точек, лежащих на равном удалении от концов данного отрезка AB, - серединный перпендикуляр.
Д-во в одну сторону: рассмотрим серединный перпендикуляр. Возьмем на нем любую точку X. В треугольнике AXB совпадают медиана и высота, тогда он равнобедренный, и XA = XB.
В другую сторону: пусть нашлась точка X, равноудалённая от концов отрезка и не лежащая на серединном перпендикуляре. Опустим перпендикуляр из точки Х. По условию треугольник равнобедренный, так что основание перпендикуляра - середина AB. Имеем две несовпадающие высоты, проходящие через одну точку. Противоречие.
Итак, все точки, равноудалённые от концов отрезка, лежат на серединном перпендикуляре (на деле, мы доказали даже чуть больше). Так как через две точки можно провести ровно одну прямую, то через две точки M и N, лежащие на серединном перпендикуляре, проходит только серединный перпендикуляр.