1)В треугольнике ABC угол A тупой , BK и СD - высоты, BK = 12 см, AK = 9 см, CD = 10 см....

Question

1)В треугольнике ABC угол A тупой , BK и СD - высоты, BK = 12 см, AK = 9 см, CD = 10 см. Найдите площадь треуг. ABC.(В чертеже высоты BK и CD идут вне треугольника).
2) В ромбе ABCD, AC = 10 дм, BD = 24 дм.Высота AK проведена к стороне BC. Найдите AK.( записать 2 формулы площади ромба и из 2-ой найти высоту).Найдите площадь треуг. AOM, если О - точка пересечения диагоналей, М - середина стороны AB.
Решите плиз))) Если возможно с чертежами)) :) Заранее спс)

Answer 1

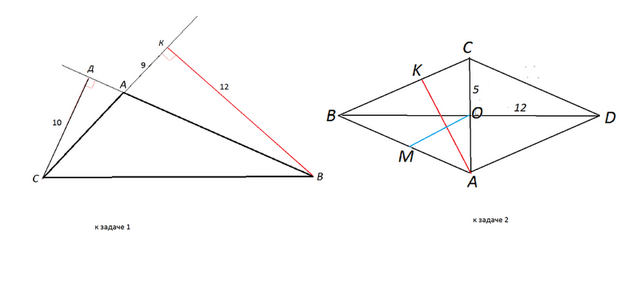
1)Площадь треугольника равна половине произведения его высоты на основание, к которому она проведена. 
Из треугольника АКВ найдем АВ. Можно применить теорему Пифагора, но  ясно видно, что это треугольник "египетский" ( стороны относятся как 3:4:5), и
АВ равна 5*3=15 см ( проверьте по Пифагору). 
Итак, имеем основание АВ, высоту СД. 
S=10*15:2=75 см²  
2)
а)Площадь ромба равна половине произведения его диагоналей.
 б)Площадь ромба равна произведению высоты на его сторону.
 а)S=dD:2=10*24:2=120 см² 
б)S=ah
 h=S:a 
а=13 (прямоугольные треугольники, в которых катеты - половины диагоналей, а гипотенузы - стороны ромба - из троек Пифагора. Можно проверить по теореме Пифагора) 
h=120/13 
АК=120/13
-----------
Медиана треугольника делит его на два равновеликих ( их площади равны). 
Площадь треугольника АОМ равна половине площади прямоугольного треугольника АОВ, площадь которого, в свою очередь, равна 1/4 площади ромба. 
S AOM=S ABCD:4:2= 15 cм² 

---