начальная точка по оси х равна хо=4cos(п/6 *0)=4сos0= 4 cmпо оси у: уо=9sin(п/6*0)+3=0+3=3 cm
в эту же точку(4;3) тело вернется через (фунция периодична, значит в той же точке
будет в момент, когда время будет 12п/6(2п), то есть через 12 с) 12 с
через одну секунду координата: х1=4cos(п/6 *t)=4cos(п/6*1)=4сos п/6=3.5 cmy1=9sin(п/6*1)+3=7.5 cm
через две секунды : x2=4cos(п/6 *2)=4cos(п/3)=2 cm y2=9sin(п/6*2)+3=9*0.86+5=10.8 cm
через три секунды: x3=4cos(п/6 *3)=4cos(п/2)=0 cm y3=9sin(п/6*3)+3=9*1+5=14 cm
через 6 с : x6=4cos(п/6 *6)=4cos(п)=-1 cm y6=9sin(п/6*6)+3=9*0+3=3 cm
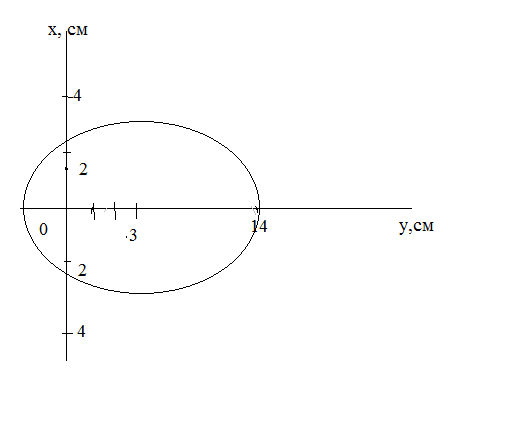
далее идет симметрично отностительно прямой у=3 (во вложениях
график)
Траектория:овал
(радиус по горизонтали 11 см, по вертикали 4)
скорость точки в момент времени 1с равна производной пути по
оси х и оси у
vx=x"(1)=( 4cos(п/6 *1))" = 4*sin п/6 = 2 см/с
vy=y"(1)=(
9sin(п/6*1)+3)"=9*cosп/6=7.8 см/с
по теореме пифагора
v^2=vx^2+vy^2=2^2+7.8^2=64.84
v=8.1
см/с
ускорение в этом случае центростремительное,
a=v^2/R
в момент времени 1с радиус равен R^2=(хо)^2+(y1-yo)^2=(3.5)^2+(7.5-3)^2=32.5см
R=5.7см
- это и есть радиус кривизны
ац=8.1^2/5.7=11.5 /с^2
в момент времени равно 0 скорость равна vx=x"(0)=4sin0= 0 см/сvy=y”(0)=9cos0=9 cm/c
тогда v=9
см/с
касательное ускорение: aк = v1-vo/t1=8.1-9/1=-0.9 см/с2
нормальное ускорение : а^2=aц(0)^2+ак^2
ац(0)=vo^2/Ro(макс.радиус
овала по вертикали)=9^2/4=20.25см/с2 -
центростремит.ускорение в момент времени 0
a^2=20.25^2+(-0.9)^2=410.9 см/с2
a=20.3 см/с