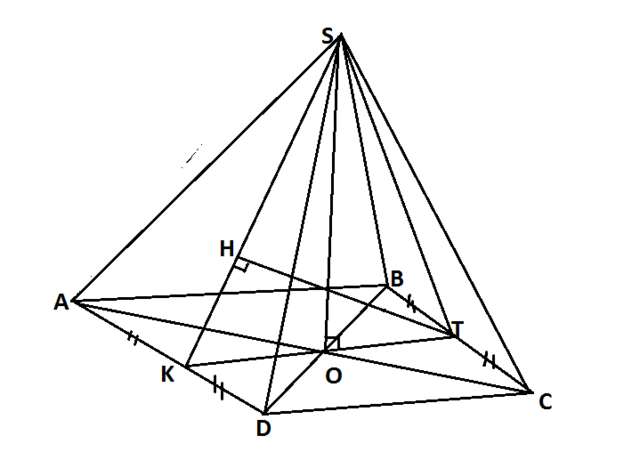
SO = 2 - высота,
О - пункт пересечения диагоналий основания- квадрата АВСД
ВД = АС = АД √2 = 4√2 (как диагональ квадрата со стороной 4 )
ВО = ОД = ВД/2 = 2√2
по т. Пифагора SD = √(SO² + OD²) = 2√3
ΔASD -равнобедренный, в нем проводим высоту SK к стороне АД
SK еще будет и медианой⇒ АК = КД = АД/2 = 2
по т. Пифагора SK = √SD² - KD²) = 2√2
пускай Т - середина стороны ВС
проведем в треугольнике SKT высоту ТН к стороне SК, она и будет расстояние от прямой BC до боковой грани SAD
КТ = АВ = 4
Sskt = SO * KT * 1/2 = 4
TH = 2S/SK = 4/(2√2) = √2
_________________________________________________________
рисунок во вложении