1
РЕШЕНИЕ
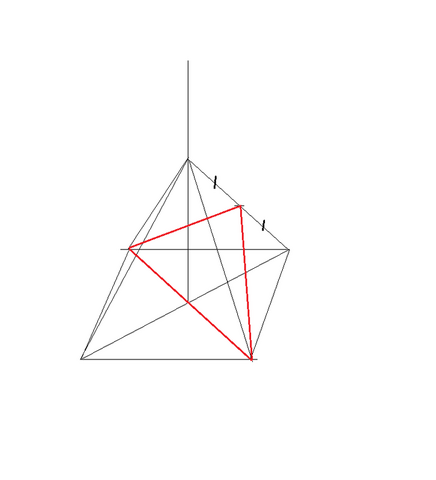
рисунок прилагается
В четырехугольной пирамиде SABCD все ребра равны,значит все боковые грани равносторонние треугольники
Так как точка M -- середина ребра SC, то
ВМ - медиана, биссектриса, высота в треугольнике BSC и
ВМ -перпендикуляр к SC
DМ - медиана, биссектриса, высота в треугольнике DSC и
DМ -перпендикуляр к SC
ТРИ точки B,D,M образуют плоскость BMD, в которой лежат пересекающиеся прямые (BM) и (DM).
Так как (SC) перпендикулярна к каждой из прямых (BM) и (DM),
следовательно плоскость BMD перпендикулярна прямой SC.
ДОКАЗАНО.
2
РЕШЕНИЕ
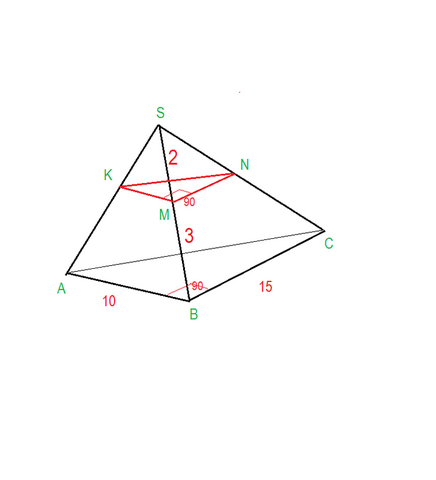
рисунок прилагается
Так как АВ ⊥ ВС , то основание пирамиды - прямоугольный треугольник ABC
площадь прямоугольного треугольника S(∆ABC)=1/2 АВ*ВС = 1/2 *10*15=75
Так как через точку М ребра SB проведено сечение плоскостью, параллельной плоскости АВС, то по теореме Фалеса эта плоскость делит боковые ребра пирамиды на пропорциональные отрезки таким образом, что:
∆ASB ~ ∆KSM
∆ASC ~ ∆KSN
∆BSC ~ ∆MSN
подобные треугольники.
Искомое сечение ∆KMN
Причем если SM:MB=2:3 , то коэффициент подобия k = SM/SB = 3/5
В подобных треугольниках соответствующие стороны пропорциональны
KM ~ AB
KN ~ AC
MN ~ BC
тогда ∆KMN ~ ∆ABC с коэффициентом подобия k = 3/5 .
Известно, что площади подобных треугольников относятся, как k^2 тогда
S(∆KMN) = k^2 * S(∆ABC) = (3/5)^2 * 75 = 27
ответ S = 27