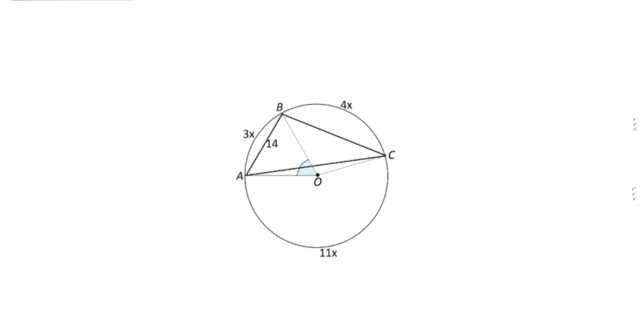
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11.
Пусть коэффициент отношения дуг равен k
Тогда градусная мера окружности содержит
3k+4k+11k=18k градусов
18k=360°
k=20°
Соединим центр окружности с вершинами треугольника АВС
∠ АОВ=3k=3*20°=60°,
∠ ВОС=4k=4*20°=80°
∠ АОС=11k=11*20°=220°
Углы треугольника АВС - вписанные и равны половине соответственного каждому центрального угла.
Меньшая сторона треугольника лежит против меньшего угла.
Меньший угол треугольника равен половине меньшего центрального угла: АОВ:2=60:2=30°.
Треугольник АОВ равнобедренный ( АО=ВО - радиусы), но и равносторонний, т.к. углы при АВ равны (180-60):2=60°
Следовательно, радиус окружности равен АО=ВО=АВ=14