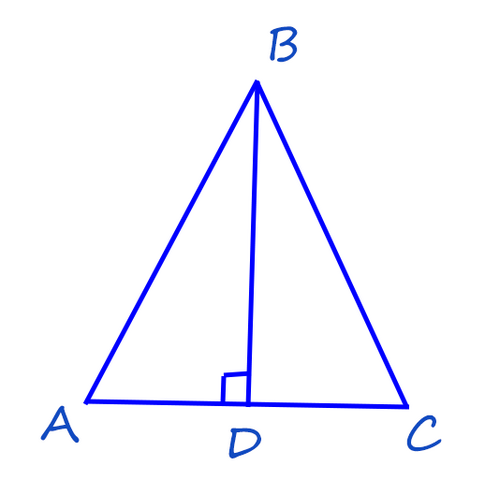
Рассмотрим любой не равнобедренный треугольник АВС, у которого высота и медиана из точки В совпадают. Обозначим этот отрезок BD.
Рассмотрим треугольники ABD и CBD.
* Они прямоугольные, т.к. ВD - высота.
* AD=CD т.к. BD - медиана, делит AC пополам.
* ВD - общая сторона
Следовательно, треугольники равны по двум катетам.
У равных треугольников соответствующие величины равны, значит, AB=BC, а значит треугольник равнобедренный.
Итог: изначально мы предположили, что данный треугольник не равнобедренный, и доказали обратное. Значит, любой треугольник с совпадающей высотой и медианой - равнобедренный. Что и требовалось доказать.