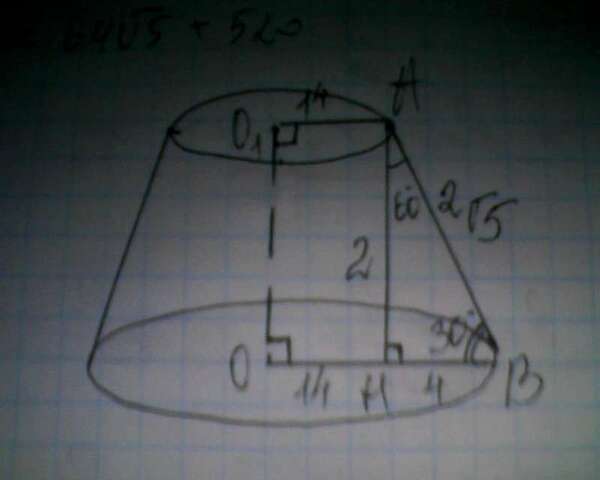
В усеченном конусе будет образована прямоугольная трапеция, если проведем высоту, получится прямоугольный треугольник с углом 30 при основании. (рисунок) Так как 14- верхний радиус, то снизу будет 14 и 4. 4 - нижний катет треугольника. катет напротив угла 30 град=1/2 гипотенузы = 2. По т. Пифагора можем найти гипотенузу (она же и образующая) из треугольника АВН: АВ²=АН²+НВ²=2²+4²=4+16=20. АВ=√20=2√5
Площадь полной поверхности усеченного конуса= π*(L*R1+L*R2+R1²+R2²) (L-образующая) S=π(2√5*14+2√5*18+14²+18²)=64√5π+520π