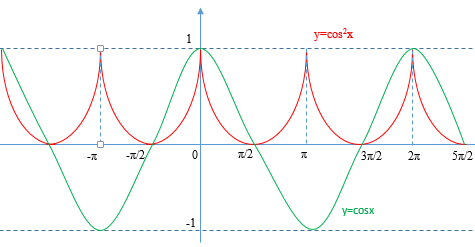
Пусть z=cosx. Тогда данная ф-я предтавится в виде y=z². При z=1 значения z и у совпадают. При других положительных значениях z точки у будут лежать ниже, т.к. z<1. График ф-ии у будет представлять периодически повторяющие кусочки. Построим его. Глядя на него легко определить промежутки монотонности.<br>Ответ:
на [π/2+πk; π+πk] функция возрастает, k - любое число;
на [π+πn; 3π/2+πn], функция убывает, n - любое число.
Скорее всего, вид будет немного другим, как показано на втором рисунке, но это несущественно
Стандартный способ:
y'=-2cosx·sinx
2cosx·sinx=0
1) cosx=0 x=π/2+πk
2) sinx=0 x=πk
Общее решение x=πk/2
Заполняем таблицу от 0 до π
0;π/2 π/2;π π;3π/2 3π/2;π
y' - + - +
y убыв возр убыв возр
Итак, ф-я убывает на [0+πk;π/2+πk]
(0 конечно можно не писать, это что б понятнее быдо как получили)
возрастает на [π/2+πn;π+πn]