Может показаться, что одна диагональ не может отсечь от трапеции равнобедренный прямоугольный треугольник, если гипотенуза в нем - меньшее основание.Такое должно быть возможно только в паре со второй диагональю.
Но трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны.
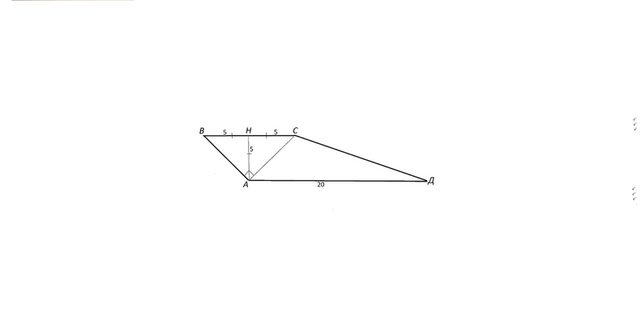
Нарисуем трапецию АВСД, отвечающую условию задачи.
Отложим большее основание АД и из А возведем перпендикуляр АН.
Он будет высотой равнобедренного прямоугольного треугольника ВАС, проведенной из вершины прямого угла ВАС к меньшему основанию ВС
( гипотенузе треугольника ВАС), т.к. треугольник равнобедренный, и будет также высотой трапеции.
Высота АН является и медианой - треугольник равнобедренный,- а медиана прямоугольного треугольника равна половине гипотенузы:
h=10:2=5 см.
Теперь осталось вычислить площадь трапеции, которая равна произведению ее высоты на полусумму оснований:
S=h(a+b):2
S=5*(10+20):2=75 см²
Рисунок во вложении.