А ларчик то просто открывался, вовсе бесхитростные и безобидные задачки))
№1
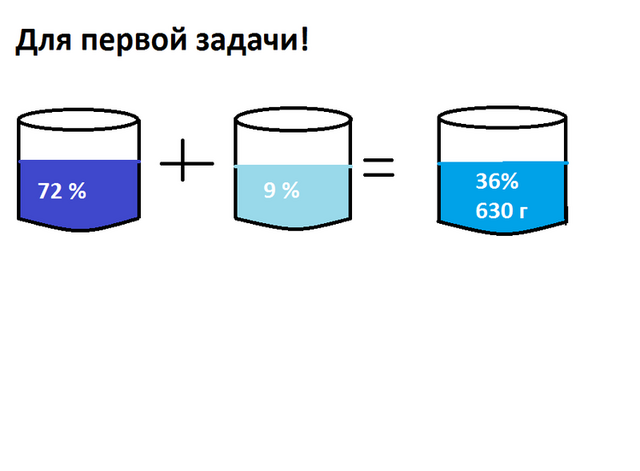
Пусть масса 72% раствора х грамм, а масса 9 % раствора у грамм, тогда, массу третьего раствора можно отобразить вот таким выражением(на картинке очень хорошо это понятно)
х +у = 630
Теперь, если масса 72% раствора х грамм, то масса кислоты в этом растворе будет 0,72х грамм.
Если масса 9% раствора у грамм, то масса кислоты будет в нем 0,09у грамм
В третьем растворе 0,36*630 грамм, не будем до конца досчитывать 0,36*630, потому что:
Так же как и для масс растворов, для масс кислот в этих раствора будет верно равенство:
0,72х + 0,09у = 0,36*630, теперь поделим все это выражение на 0,09 и получим:
8х + у = 2520
Из двух уравнений(я выделил их жирным шрифтом) составим системку и решим ее.
из первого уравнения вычтем второе и получим:
7х = 1890
х = 270 грамм, отсюда:
у = 630г - 270г = 360г
Ответ: Для приготовления 630г 36% раствора нужно взять 270г 72% раствора и 360г 9% раствора серной кислоты.
Вторая задача того проще)
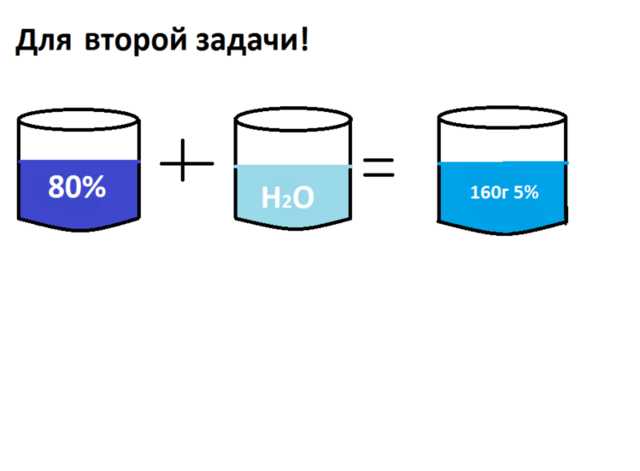
Рисунок тоже приляпал)
Раствор нужно разбавить.
Рассчитаем массу кислоты в 5% растворе:
m(кислоты) = w*m(р-ра) = 0,05*160г = 8 г
Т.к. происходит разбавление, то в 80% растворе будет содержаться столько же кислоты, сколько ее содержится в 5% растворе массой 160г
Рассчитаем массу раствора 80%
m(р-ра) = m(кислоты)/w = 8г/0,8 = 10г
m(воды) = m(получ. р-ра) - m(исх. р-ра) = 160г - 10г = 150г
Ответ: для приготовления 5% раствора уксуса массой 160г нужно взять 10г уксусной эссенции и 150г воды.
