В параллелограмме АВСД точка М - середин стороны АВ. Известно, что МС=МД. Докажите, что...

Question

В параллелограмме АВСД точка М - середин стороны АВ. Известно, что МС=МД. Докажите, что данный параллелограмм - прямоугольник.

Answer 1

Нарисуйте параллелограмм.  Проведите в нем среднюю линию МН.

Соедините В и Н. 

Теперь у вас есть параллелограмм МВСН, с  диагоналями МС И ВН,   а ВН=МД как равные диагонали в равных параллелограммах МВСН и АМНД. 

Поэтому диагонали параллелограмма МВСН равны между собой по условию задачи.

Диагонали равны в параллелограмме, если он - прямоугольный. Параллелограмм АВСД - прямоугольник.  

 

Answer 2

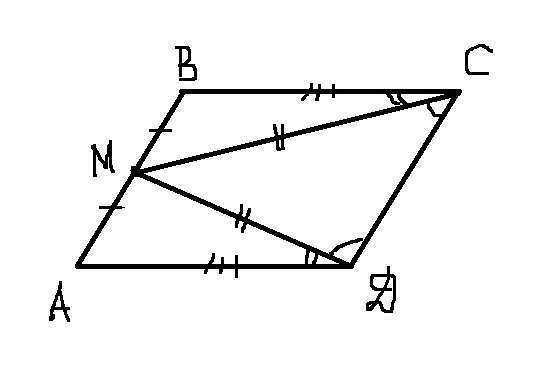
треугольник DMC - равнобедренный, значит углы при основании равны угол MCD = угол MDC

треугольник MBC = треугольник AMD по трем сторонам (MC = MD, AM = MB, BC = AD)

тогда соответствующие углы равны угол ADM = угол BCM

т.е. угол BCD = угол ADC, следовательно ABCD - прямоугольник

 

---