В параллелограмме KLMN точка B - середина стороны KN. Известно, что BL=BM. Докажите, что...

Question

В параллелограмме KLMN точка B - середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм - прямоугольник.

Answer 1

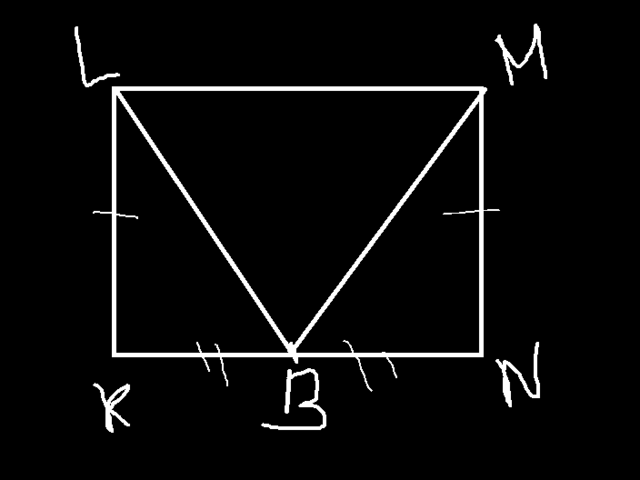
Дано: KLMN - параллелограмм

В принадлежит KN,KB=BN

BL=BM

Док-ть:

т.к. KLMN - параллелограмм,то 

KL=MN.

ПО условию KB=BN

BL=BM

След-но,треугольник KLВ= треуг.NMB по трем сторонам.Значит,угол К= углу N,как соответственные углы равных треугольников.По свойству   параллелограмма KL||MN 

 

KN-секущая,то угол К+ угол N = 180

Таким оьразом 

угол К = углу N 

180 : 2 = 90 

 

---