Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия...

Question

Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия трапеции равна 14 см, боковая сторона равна 4 корня из 2, а одно из оснований трапеции является диаметром описанной окружности

Answer 1

Рассмотрим два подобных прямоугольных треугольника ОРЕ и ОЕD; РО - половина средней линии m = 14; OD = R - радиус окружности, ED = CD/2 = b/2, где b = 4*корень(2) - боковая сторона. 

EP/OE = OE/OD; OD*EP = OE^2 = OD^2 - ED^2;

R^2 - R*m/2 - (b/2)^2= 0; 

R^2 - R*7 - 8 = 0; R = 8 (второй корень -1 отброшен)

Answer 2

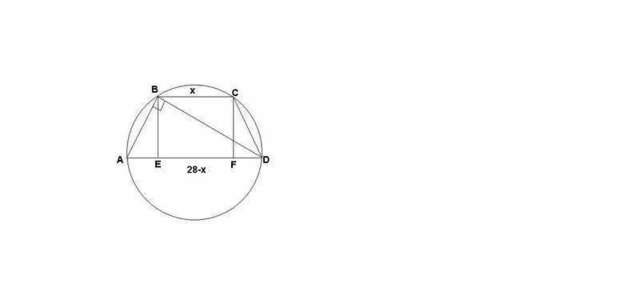
Следует отметить, что описать окружность можно только около равнобедренной трапеции. Кроме того, так как AD диаметр, то угол ABD =90(опирается на диаметр)

Проведем ВЕ и CF перпенд. AD, тогда AE=FD

Средняя  линия=14, значит AD+BC=28

Пусть ВС=х. тогда AE=(28-x-x):2=14-x

AB^2=AE*AD( свойство перпендикуляра опущенного из вершины прямого угла на гипотенузу)

16*2=(14-х)(28-х)

x^2-42х+360=0

D=324

x1=30 не походит

x2=12

AD=28-12=16

AD диаметр, значит радиус 8

 

---