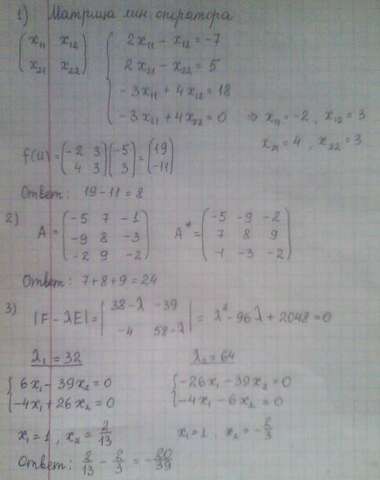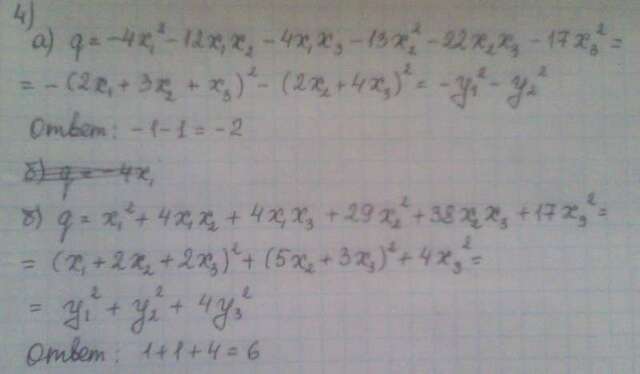Помогите, пожалуйста, решить, хотя бы что-то:
1) Для линейного оператора f известно, что f 2 = -7 и f - 3 = 18
-1 5 4 0
Найдите значение этого линейного оператора на векторе u= -5 . В ответе укажите сумму координат вектора f(u). 3
2) Известно, что в некотором ортонормированном базисе
f х1 -5х1+7х2-х3
х2 = -9х1+8х2-3х3
х3 -2х1+9х2-2х3 . Найдите матрицу оператора f* сопряженного для f. В ответе укажите сумму 2-й строки.
3) Найдите собственные значения и собственные векторы линейного оператора f, если известна его матрица в стандартном базисе
F= 38 -39
-4 58 . Первые координаты собственных векторов приравняйте к 1. В ответе укажите сумму их вторых координат.
4) Методом Лангранжа приведите квадратичную форму:
а) q=-4x1^2-12x1x2-4x1x3-13x2^2-22x2x3-17x3^2
б) q= x1^2+4x1x2+4x1x3+29x2^2+38x2x3+17x3^2
к нормальному виду. В ответе укажите сумму коэффициентов нормального вида.
5) Классифицируйте квадратичную форму по знаку:
а) q=22x1^2-10x1x2+16x1x3+2x2^2-8x2x3+16x3^2
б) q=11x1^2-34x1x2-8x1x3+7x2^2+16x2x3+4x3^2