1.
Sромба = S прям.
18 · 7 = 14 · х, где х - неизвестная сторона прямоугольника.
х = 18 · 7 /14 = 9 см
P = 2(14 + 9) = 2·23 =
46 cм
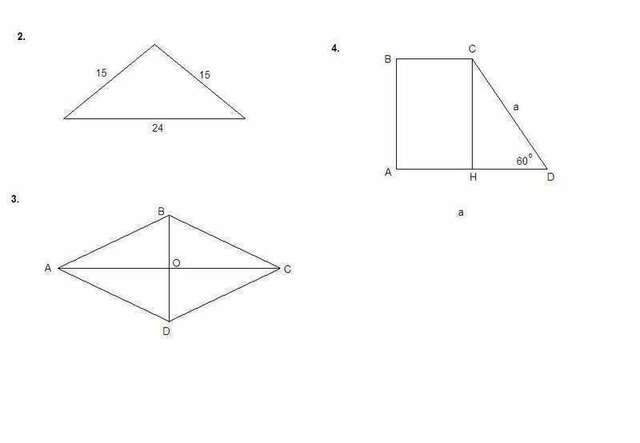
2.
Р = 15 + 15 + 24 = 54 см - периметр треугольника
р = 27 см - полупериметр.
По формуле Герона:
S = √(p(p - 15)(p - 15)(p - 24)) = √(27·12·12·3) = 12 · 9 =
108 см²
3.
ΔABD: AB = AD как стороны ромба, ∠BAD = 60°, значит, треугольник равносторонний.
AB = AD = BD =
12 см.
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
BO = OD = 6 см
ΔАОВ: по теореме Пифагора
АО = √(АВ² - ВО²) = √(144 - 36) = √108 = 6√3 см
АС = 2АО
= 12√3 см
4.
Проведем высоту трапеции СН.
ΔHCD: ∠CHD = 90°, ∠CDH = 60°, ⇒ ∠HCD = 30°, тогда
DH = a/2 как катет, лежащий напротив угла в 30°.
по теореме Пифагора СН = √(CD² - DH²) = √(a² - a²/4) = a√3/2.
АН = AB - HD = a/2.
СН = АВ как высоты, СН║АВ как перпендикуляры к одной прямой, значит АВСD - прямоугольник.
BC = AH = a/2
Sabcd = (AD + BC)/2 · CH = (a + a/2)/2 · a√3/2 = 3a/4 ·a√3/2
= 3a²√3/8