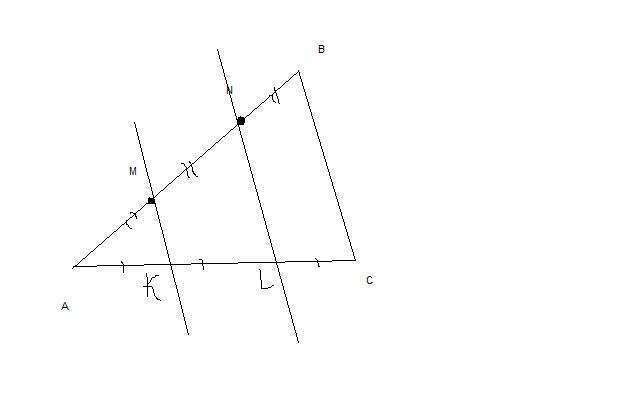
Обозначим точки пересечения прямых с стороной AC через K и L.AK=KL=LC по теореме Фалеса.AN =2/3 от AB а AL 2/3 от AC. Треугольник ABC подобен ANL подобен AMK.Так как прямые параллелны и соответсвенные углы равно.
Коэффициент подобия для треугольников ANL и ABC равен 2/3:1=2/3
Площади этих треугольников относятся друг другу как квадрат коэфициента подобия тоесть 4/9. S1/S2=4/9. S1 - площадь ANL а S2 площадь ABC. Так как площадь ABC известно и оно ранво 1 то площадь S1=4/9.Таким же образом найдем площадь S3 треугольника AMK. Она равна 1/9. Smkln=S1-S3=3/9