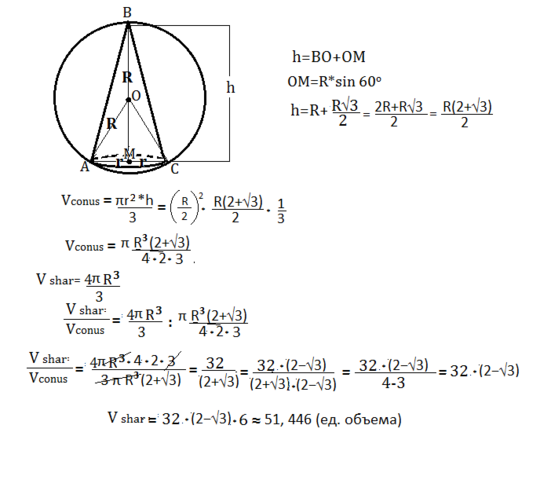
Подобные задачи чаще даются с радиусом конуса, равным радиусу шара.
Т.к. диаметр основания конуса равен радиусу шара, радиус основания конуса равен половине радиуса шара, т.е. R/2
Высота конуса равна радиусу шара плюс высота правильного треугольника со сторонами, равными радиусу шара ( см. рисунок).
Формула объема шара
V=4πR³/3
Формула объема конуса
V=πr²h/3
1) Вычислим объем конуса, подставив в формулу радиус и высоту, выраженные через R.
2) Разделив выражение объема шара на найденный объем конуса, вычислим во сколько раз объем шара больше объема данного конуса.
3) Умножив 6 ( объем конуса) на число отношения объемов, получим объем шара.
Вычисления даны в приложении.
Результат:
объем шара равен 192*(2-√3) или ≈51,446 (ед. объема)