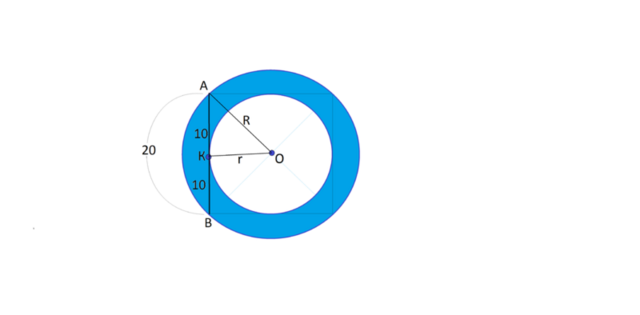
Даны две окружности с общим центром. Отрезок АВ с концами на большей окружности имеет длину 20 см и касается меньшей окружности. Тогда площадь кольца между окружностями равна ?
---------------------------------------------------------------
Площадь кольца равна разности между площадью круга с большим радиусом и площадью круга с меньшим радиусом.
Пусть радиус большего круга равен
R, а меньшего -
r.
Тогда площадь большего круга равна πR², а меньшего πr².
а площадь кольца S-s= πR²-πr²
Соединив общий центр окружностей с концом А касательной АВ и с точкой касания К, получим прямоугольный треугольник АКО. с гипотенузой
R и катетами
r и
AK
По т. Пифагора R²-r²=AK²
R²-r²=100
πR²-πr²=π(R²-r²)
Но (R²-r²)=100.
Следовательно,
площадь кольца между окружностями равна 100 π см²
----------
[email protected]