Из точки М проведен перпендикуляр МВ , равный 4 см, к плоскости прямоугольника...

Question

Из точки М проведен перпендикуляр МВ , равный 4 см, к плоскости прямоугольника АВСD.Наклонные МА и МС образуют с плоскостью прямоугольника углы в 45º и 30º соответственно.
а) докажите, что треугольники МAD и MDC прямоугольные;
б) найдите стороны прямоугольника;
в) докажите, что треугольник ВDС является проекцией треугольника МDС на плоскость прямоугольника, и найдите его площадь.

Answer 1

а) 

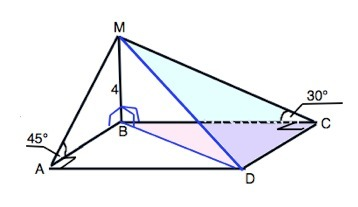
ABCD - прямоугольник. МВ перпендикулярна плоскости АВСD. 

МА - наклонная, АВ - ее проекция. АВ⊥АD. 

По т.о 3-х перпендикулярах МА⊥AD ⇒ ∆ МАD- прямоугольный. 

МС - наклонная, – ВС её проекция. 

По т.о 3-х перпендикулярах МС⊥СD – ∆ МСD- прямоугольный. ч.т.д.

б) 

АВ=МВ:tg45°=4:1=4 (см)

ВС=MB:tg30°=4:(1/√3)=4√3

CD=AB=4;  AD=BC=4√3

в)

MD - наклонная, BD - её проекция. 

ВС - проекция наклонной МС.⇒

∆ BDС - проекция ∆ MDС на плоскость АВСD. 

S∆ BCD=BC•CD:2=4√3•4:2=8√3 см²

---