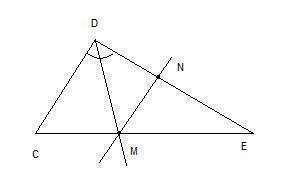
1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то
2. Зная, что развернутый угол равен 180°, находим угол DNM:
3. Поскольку DM - биссектриса, то угол MDN = 4. Зная два угла треугольника DMN, находим неизвестный угол:
°