Из точки, отстоящей от плоскости ** расстоянии 3 см, проведены две наклонные, образующие...

Question

Из точки, отстоящей от плоскости на расстоянии 3 см, проведены две наклонные, образующие с плоскостью углы 30 градусов и 60 градусов. Угол между проекциями наклонных равен 120 градусам. Найдите расстояние между основаниями наклонных. Please? Help me. Its very important for me! Необходим чертеж)

Answer 1

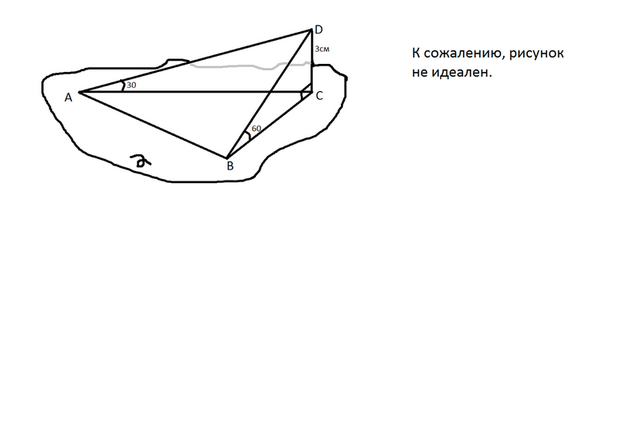
Если спроектировать 2 наклонные получаем пирамиду с высотой 3 см. Основание ABC, DC-высота. 2 боковые грани(ADC,BDC) пирамиды - прямоугольные треугольники, зная углы найдем стороны:
sin60=√3/2=DC/BD, BD=3/(√3/2)=2*√3; BC=√((2√3)^2-3^2)=√3;
sin30=1/2=DC/AD, AD=3/(1/2)=6; AC=√(6^2-3^2)=3√3;
Далее нам уже известен угол 120 и 2 стороны основания AC=3√3, BC=√3, воспользуемся теоремой косинусов:теорема тригонометрии, утверждающая, что квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними;
То есть AB=√((3√3)^2+(√3)^2-2*√3*3√3*(-0.5))= 39.

---

Comments

Сейчас рисунок сделаю.

---

Thank you, very much!!!!)

---

:)