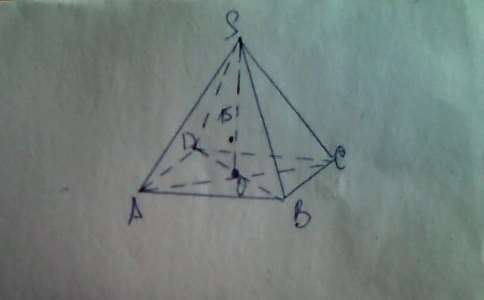
1) В основании SABCD - квадрат, в диагональном сечении - треугольник.
2)S(ASC) = 1/2*SO*AC
15/2 AC=120
AC=16
3) Находим сторону основания квадрата( по теореме Пифагора, из треугольника АВС): 2АВ^2 = 256
AB^2=128
3) Находим объем пирамиды SABCD:
V=1/3 Sосн * h
V= (AB^2*SO)/3=(128*15)/3=640