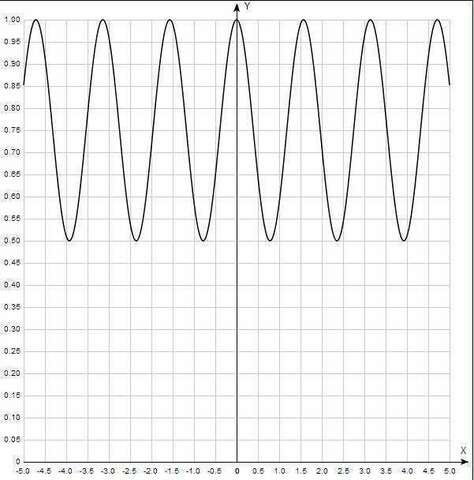
F(x) =sin^4 x + cos^4 x +2sin^2 cos^2 - 2sin^2 cos^2 =(sin^2 x + cos^2)^2 - 1/2 * 4sin^2 xcos^2 x = 1 -1/2 sin^2 (2x)
sin^2 (2x) принимает наим значение 0 наиб значение 1
Тогда f = 1 - 1/2 *0=1 наиб
f = 1 - 1/2 *1=0.5 наим
sin^2 (2x) =1 откуда sin (2x)=1 и sin (2x) = - 1
2x=(+/-) pi/2 +2pi*k
x=(+/-)pi/4 +pi* k точки, где функция принимает наим значения
sin^2 (2x) = 0 sin 2x =0 2x=pi*n x = pi /2 * n в этих точках функция принимает наиб значения