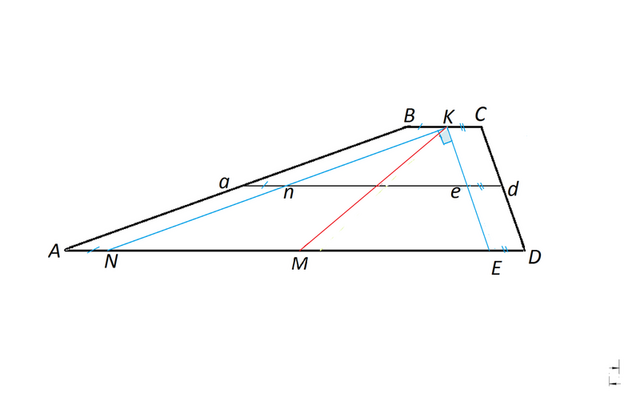
В трапеции ABCD с основаниями BC и AD угол BAD = 25°, угол CDA = 65° , средняя линия равна 10, а длина отрезка, соединяющего середины оснований, равна 8. Найдите длину основания AD
Обратим внимание на углы при большем основании.
Их сумма
25°+65°=90°.
Из середины основания ВС параллельно боковым сторонам проведем к АD прямые КN и КЕ.
Углы получившегося треугольника NКЕ также равны 25° и 65° - как соответственные при пересечении параллельных прямых секущей АD,
их сумма 90°,
угол NКЕ=90°.
КМ в прямоугольном треугольнике NKE-
медиана, т.к. по условию соединяет середины оснований трапеции.
В прямоугольном треугольнике медиана из прямого угла равна половине гипотенузы.
NЕ=2 КМ=8*2=
16.
Средняя линия
ne треугольника NКЕ принадлежит средней линии
ad трапеции и
ne=NЕ
:2=
8
ad=10,
ad-ne=10-8=
2
АN+ЕD=ВС как стороны параллелограммов.
an+ed=BK+KC=
BC=2
ВС=2
AD=ad*2-BC=20-2=
18
--------------------
Решение будет гораздо короче, если помнить, что
отрезок, соединяющий середины оснований трапеции, в которой сумма углов при большем основании равна 90°, равен полуразности оснований.
(АД-ВС)
:2=8
(АД+ВС)
:2=10 ⇒
Сложим получившуюся систему уравнений:
|АД-В=16
|АД+ВС=20
2АД=36
АД=18
---
[email protected]