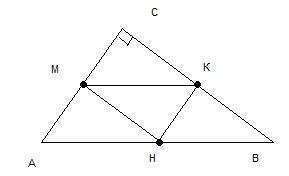
Дано:
АВС - прямоугольный
АС = 3 см
ВС = 4 см
МК, КН, МН - средние линии
Найти Рмнк
1. По теореме Пифагора находим гипотенузу треугольника АВС:
АВ = √АС²+ СВ² = √4²+ 3²= √25 = 5 см
2. Зная, что средняя линия треугольника параллельна одной из сторон треугольника и равна половине этой стороны, находим длины отрезков МК, КН и МН:
МК II AB, MK = AB : 2, MK = 5 : 2 = 2.5 см
КН II AC, KH = AC : 2, KH = 3 : 2 = 1.5 см
МН II BC, MH = BC : 2 = 4 : 2 = 2 см
3. Находим периметр МНК:
Р мнк = МК + КН + МН = 2,5 + 1,5 + 2 = 6 см